吉林省长春市绿园区2020年中考数学二模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 下列各数,最小的数是( )A、﹣2020 B、0 C、 D、﹣12. 某集成电路制造有限公司已于2019年第三季度成功量产了第一代 纳米 工艺,这是国内第一条 工艺生产线,已知 为 米,数据 用科学记数法表示为( )A、 B、 C、 D、3. 下列四个选项中,不是正方体展开图形的是( )A、
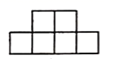 B、
B、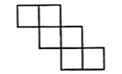 C、
C、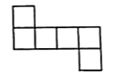 D、
D、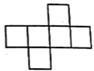 4. 不等式组 的解集是( )A、 B、 C、 D、5. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、86. 如图,从 外一点 引圆的切线 切点为 连结 并延长交 于点 连结 .若 则 的度数是( )
4. 不等式组 的解集是( )A、 B、 C、 D、5. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、86. 如图,从 外一点 引圆的切线 切点为 连结 并延长交 于点 连结 .若 则 的度数是( ) A、 B、 C、 D、7. 如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于 AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A、 B、 C、 D、7. 如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于 AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )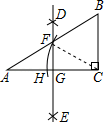 A、 B、2 C、 +1 D、2 ﹣28. 如图,点 是反比例函数 与 的一个交点,图中阴影部分的面积为 则反比例函数的解析式是( )
A、 B、2 C、 +1 D、2 ﹣28. 如图,点 是反比例函数 与 的一个交点,图中阴影部分的面积为 则反比例函数的解析式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 因式分解: .10. 关于 x 的一元二次方程 有两个相等的实数根,则 k 的值为 .11. 如图,在平面直角坐标系 中,以原点为位似中心线段 与线段 是位似图形,若 , , ,则 的坐标为 .
 12. 如图,正方形ABCD内接于⊙O,⊙O的半径为6,则 的长为 .
12. 如图,正方形ABCD内接于⊙O,⊙O的半径为6,则 的长为 . 13. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为 米,则他在不弯腰的情况下在大棚里横向活动的范围是米.
13. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为 米,则他在不弯腰的情况下在大棚里横向活动的范围是米. 14. 如图,一根竖直的木杆在离地面3.1 处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 . (参考数据: )
14. 如图,一根竖直的木杆在离地面3.1 处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 . (参考数据: )
三、解答题
-
15. 先化简,再求值: ,其中 .16. 第一盒中有2个白球、1个黄球,第二盒中有1个白球、1个黄球,这些球除颜色外无其他差别.分别从每个盒中随机取出1个球,求取出的2个球中有1个白球、1个黄球的概率.17. 如图,正方形网格中的每个小正方形的边长都是 每个小格的顶点叫格点.已知点 在格点,请在给定的网格中按要求画四边形,使四边形的四个顶点都在格点.
 (1)、以 为顶点在图甲中画一个面积为 的中心对称图形且满足 ;(2)、以 为顶点在图乙中画一个周长为 、面积为 的四边形,使其既是轴对称图形,又是中心对称图形.18. 某超市投入1380元资金购进甲、乙两种矿泉水共50箱,矿泉水的成本价和销售价如表所示:
(1)、以 为顶点在图甲中画一个面积为 的中心对称图形且满足 ;(2)、以 为顶点在图乙中画一个周长为 、面积为 的四边形,使其既是轴对称图形,又是中心对称图形.18. 某超市投入1380元资金购进甲、乙两种矿泉水共50箱,矿泉水的成本价和销售价如表所示:类别/单价
成本价(元/箱)
销售价(元/箱)
甲
24
36
乙
33
48
(1)、该超市购进甲、乙两种矿泉水各多少箱?(2)、全部售完50箱矿泉水,该超市共获得利润多少元?19. 已知:如图,在 中, 是 的中线, 为 的外角 的平分线, 交 于点 . (1)、求证:四边形 是矩形;(2)、若 ,当 的周长为 时,矩形 的面积是20. 为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(1)、求证:四边形 是矩形;(2)、若 ,当 的周长为 时,矩形 的面积是20. 为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5
75.5~80.5
80.5~85.5
85.5~90.5
90.5~95.5
95.5~100.5
男生
1
1
1
5
5
2
女生
0
1
2
3
7
2
(分析数据)
(1)、两组样本数据的平均数、众数、中位数、方差如下表所示:性别
平均数
众数
中位数
方差
男生
90
90
90
44.9
女生
90
32.8
在表中: . ;
(2)、若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?(3)、通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.21. 某贮水塔在工作期间,每小时的进水量和出水量都是固定不变的.从凌晨4点到早8点只进水不出水,8点到12点既进水又出水,14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y(立方米)与x(时)的函数图象.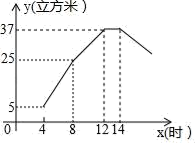 (1)、求每小时的进水量;(2)、当8≤x≤12时,求y与x之间的函数关系式;(3)、从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.22. 下图是华师版八年级下册数学教材第 页的部分内容.(1)、如图18.1.14,在 中,对角线 ,垂足为点 且 .求AD和BC之间的距离.
(1)、求每小时的进水量;(2)、当8≤x≤12时,求y与x之间的函数关系式;(3)、从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.22. 下图是华师版八年级下册数学教材第 页的部分内容.(1)、如图18.1.14,在 中,对角线 ,垂足为点 且 .求AD和BC之间的距离. (2)、如图①,两张等宽的纸条交叉叠放在一起,在重叠部分构成的四边形 中,若 ,求点 到 的距离;
(2)、如图①,两张等宽的纸条交叉叠放在一起,在重叠部分构成的四边形 中,若 ,求点 到 的距离; (3)、如图②,在 中, ,点 为 边上的任一点(不与 重合) 为垂足,求 的值.
(3)、如图②,在 中, ,点 为 边上的任一点(不与 重合) 为垂足,求 的值. 23. 如图①,在 中, ,点 从点 出发,以每秒 个单位长度的速度沿 向终点 匀速运动,作 于 以 为边向右作正方形 设正方形 与 的重叠部分的面积为 点 的运动时间为 (秒).
23. 如图①,在 中, ,点 从点 出发,以每秒 个单位长度的速度沿 向终点 匀速运动,作 于 以 为边向右作正方形 设正方形 与 的重叠部分的面积为 点 的运动时间为 (秒). (1)、填空: , 用含 的代数式表示 则 ;(2)、当点 落在边 上时,求 的值.(3)、当正方形 与 的重叠部分图形为四边形时,求 与 的函数关系式.(4)、如图②,点 出发的同时,点 从点 出发,以每秒 个单位长度的速度沿 向终点 匀速运动,作 于 以 为斜边向左构造等腰直角 ,当 的直角顶点R落在正方形的边或对角线上时,直接写出 的值.
(1)、填空: , 用含 的代数式表示 则 ;(2)、当点 落在边 上时,求 的值.(3)、当正方形 与 的重叠部分图形为四边形时,求 与 的函数关系式.(4)、如图②,点 出发的同时,点 从点 出发,以每秒 个单位长度的速度沿 向终点 匀速运动,作 于 以 为斜边向左构造等腰直角 ,当 的直角顶点R落在正方形的边或对角线上时,直接写出 的值. 24. 在平面直角坐标系中,将函数 为常数)的图象记为G.(1)、当 时,设图象 上一点 ,求 的值;(2)、设图象 的最低点为 ,求 的最大值;(3)、当图象 与 轴有两个交点时,设右边交点的横坐标为 求 的取值范围;(4)、设 ,当图象 与线段 没有公共点时,直接写出 的取值范围.
24. 在平面直角坐标系中,将函数 为常数)的图象记为G.(1)、当 时,设图象 上一点 ,求 的值;(2)、设图象 的最低点为 ,求 的最大值;(3)、当图象 与 轴有两个交点时,设右边交点的横坐标为 求 的取值范围;(4)、设 ,当图象 与线段 没有公共点时,直接写出 的取值范围.