吉林省长春市净月高新区2020年中考数学一模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 下列实数中,是无理数的为( )A、0 B、- C、 D、3.142. 2020年“五一”假日期间,某电商平台网络交易总金额接近15亿元.其中15亿用科学记数法表示为( )A、1.5×109 B、15×109 C、1.5×108 D、15×1083. 某个几何体的展开图如图所示,该几何体是( )
 A、三棱锥 B、四棱锥 C、三棱柱 D、圆锥4. 不等式3x+3≤0的解集在数轴上表示正确的是( )A、
A、三棱锥 B、四棱锥 C、三棱柱 D、圆锥4. 不等式3x+3≤0的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、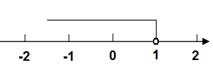 D、
D、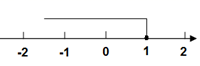 5. 如图,△ ∽△ ,若 , , ,则 的长是( )
5. 如图,△ ∽△ ,若 , , ,则 的长是( ) A、2 B、3 C、4 D、56. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若 ,则 的度数为( )
A、2 B、3 C、4 D、56. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若 ,则 的度数为( )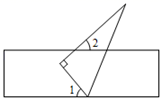 A、45° B、 C、 D、7. 如图,正五边形 内接于⊙ , 为 上的一点(点 不与点 重合),则 的度数为( )
A、45° B、 C、 D、7. 如图,正五边形 内接于⊙ , 为 上的一点(点 不与点 重合),则 的度数为( ) A、 B、 C、 D、8. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )A、 B、 C、 D、
A、 B、 C、 D、8. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )A、 B、 C、 D、二、填空题
-
9. 计算:m·(m2)3= .10. 若a﹣b= ,ab=1,则a2b﹣ab2= .11. 一元二次方程x2﹣3x+1=0的根的判别式的值是 .12. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5.则△BEC的周长是 .
 13. 如图,平行四边形ABCD中,顶点A的坐标是(0,2),AD//x轴,BC交y轴于点E,点E的纵坐标是﹣4,平行四边形ABCD的面积是24,反比例函数y= 的图象经过点B和D.则k= .
13. 如图,平行四边形ABCD中,顶点A的坐标是(0,2),AD//x轴,BC交y轴于点E,点E的纵坐标是﹣4,平行四边形ABCD的面积是24,反比例函数y= 的图象经过点B和D.则k= .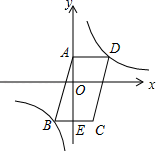 14. 如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△PAB的周长最小时,点P的坐标为 .
14. 如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△PAB的周长最小时,点P的坐标为 .
三、解答题
-
15. 先化简,再求值:(a﹣2b)2﹣(a﹣b)(a﹣3b),其中b= .16. 净月某校在抗疫期间组织志愿小组到附近敬老院为老人服务,准备从初三(1)班中的3名男生小亮、小明、小伟和2名女生小红、小丽中选取一名男生和一名女生.请用画树状图(或列表)的方法,求出恰好选中男生小明和女生小红的概率.17. 某车间接到加工960个零件的任务,在加工完160个后,由于改进了技术,每天加工的零件数量是原来的5倍,整个加工过程共用了4天完成.求原来每天加工零件的数量.18. 如图,BC为⊙O直径,点A是⊙O上任意一点(不与点B、C重合),以BC、AB为邻边的平行四边形ABCD的顶点D在⊙O外.
 (1)、当AD与⊙O相切时,求∠B的大小.(2)、若⊙O的半径为2,BC=2AB,直接写出 的长.19. 如图,在4×5的正方形网格中,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、B均在格点上,以AB为边画等腰△ABC,要求点C在格点上.
(1)、当AD与⊙O相切时,求∠B的大小.(2)、若⊙O的半径为2,BC=2AB,直接写出 的长.19. 如图,在4×5的正方形网格中,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、B均在格点上,以AB为边画等腰△ABC,要求点C在格点上. (1)、在图①、图②中画出两种不同形状的等腰三角形△ABC.(2)、格点C的不同位置有处.20. 净月某中学为了抗疫宣传,在七八年级开展了“防疫知识”大赛.为了解参赛学生的成绩情况,从两个年级中各随机抽取10名学生的成绩,数据如下:
(1)、在图①、图②中画出两种不同形状的等腰三角形△ABC.(2)、格点C的不同位置有处.20. 净月某中学为了抗疫宣传,在七八年级开展了“防疫知识”大赛.为了解参赛学生的成绩情况,从两个年级中各随机抽取10名学生的成绩,数据如下:七年级:88 94 90 94 84 94 99 94 99 100
八年级:84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:
成绩x
人数
年级
80≤x<85
85≤x<90
90≤x<95
95≤x≤100
七年级
1
1
5
3
八年级
a
1
4
4
分析数据:补全下列表格中的统计量:
统计量
年级
平均数
中位数
众数
方差
七年级
93.6
94
b
24.2
八年级
93.7
c
93
20.4
得出结论:
(1)、a= , b= , c= .(2)、由统计数据可知, 年级选手的成绩比较接近.(3)、学校规定,成绩不低于90分的选手可以获奖,若该校七年级有200人参加比赛,请估计有多少人获奖.21. 甲、乙两人在净月大街上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA﹣AB﹣BC﹣CD所示. (1)、甲的速度为米/分,乙的速度为米/分.(2)、求线段AB的表达式,并写出自变量x的取值范围.(3)、求乙比甲早几分钟到达终点?22. (教材呈现)数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:
(1)、甲的速度为米/分,乙的速度为米/分.(2)、求线段AB的表达式,并写出自变量x的取值范围.(3)、求乙比甲早几分钟到达终点?22. (教材呈现)数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下: (1)、赵老师用尺规作角平分线时,用到的三角形全等的判定方法是 .(2)、小明发现只利用直角三角板也可以作∠AOB的角平分线,方法如下:
(1)、赵老师用尺规作角平分线时,用到的三角形全等的判定方法是 .(2)、小明发现只利用直角三角板也可以作∠AOB的角平分线,方法如下:步骤一:利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.
步骤二:分别过点M、N作OM、ON的垂线,交于点P.
步骤三:作射线OP,则OP为∠AOB的平分线.
①请写出小明作法的完整证明过程.
②当tan∠AOB= 时,量得MN=4cm,直接写出 的面积.
 23. 如图①,在平行四边形ABCD中,AB=8,BC=6,∠ABC=60°.AE平分∠BAD交CD于点F.动点P从点A出发沿AD向点D以每秒1个单位长度的速度运动.过点P作PQ⊥AD,交射线AE于点Q,以AP、AQ为邻边作平行四边形APMQ,平行四边形APMQ与△ADF重叠部分面积为S.当点P与点D重合时停止运动,设P点运动时间为t秒.(t>0)
23. 如图①,在平行四边形ABCD中,AB=8,BC=6,∠ABC=60°.AE平分∠BAD交CD于点F.动点P从点A出发沿AD向点D以每秒1个单位长度的速度运动.过点P作PQ⊥AD,交射线AE于点Q,以AP、AQ为邻边作平行四边形APMQ,平行四边形APMQ与△ADF重叠部分面积为S.当点P与点D重合时停止运动,设P点运动时间为t秒.(t>0) (1)、用含t的代数式表示QF的长;(2)、当点M落到CD边上时,求t的值;(3)、求S与t之间的函数关系式;(4)、连结对角线AM与PQ交于点G,对角线AC与BD交于点O(如图②).直接写出当GO与△ABD的边平行时t的值.24. 函数y= (m为常数)(1)、若点(﹣2,3)在函数y上,求m的值.(2)、当点(m,﹣1)在函数y上时,求m的值.(3)、若m=1,当﹣1≤x≤2时,求函数值y的取值范围.(4)、已知正方形ABCD的中心点为原点O,点A的坐标为(1,1),当函数y与正方形ABCD有3个交点时,直接写出实数m的取值范围.
(1)、用含t的代数式表示QF的长;(2)、当点M落到CD边上时,求t的值;(3)、求S与t之间的函数关系式;(4)、连结对角线AM与PQ交于点G,对角线AC与BD交于点O(如图②).直接写出当GO与△ABD的边平行时t的值.24. 函数y= (m为常数)(1)、若点(﹣2,3)在函数y上,求m的值.(2)、当点(m,﹣1)在函数y上时,求m的值.(3)、若m=1,当﹣1≤x≤2时,求函数值y的取值范围.(4)、已知正方形ABCD的中心点为原点O,点A的坐标为(1,1),当函数y与正方形ABCD有3个交点时,直接写出实数m的取值范围.