吉林省吉林市2020年中考数学一模试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $| - 3 + 2 |$ 的结果是（）

A、 $- 5$ B、 $5$ C、 $- 1$ D、 $1$

查看试题解析
2. 如图所示，由7个相同的小正方体组合成一个立体图形，它的俯视图为（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、x²+2x²＝3x⁴ B、x²·x³＝x⁶ C、（x²）³＝x⁶ D、（xy）³＝xy³

查看试题解析
4. 不等式 $x + 1 < - 1$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，矩形OABC的顶点A在x轴上，点B的坐标为（1，2）．固定边OA，向左“推”矩形OABC，使点B落在y轴的点B'的位置，则点C的对应点C'的坐标为（）

A、（﹣1， $\sqrt{3}$ ） B、（ $\sqrt{3}$ ，﹣1） C、（﹣1，2） D、（2，﹣1）

查看试题解析
6. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC，若∠BCO＝α，则∠P的度数为（）

A、2α B、90°﹣2α C、45°﹣2α D、45°+2α

查看试题解析

二、填空题

7. 计算 $\sqrt{9} - \sqrt{8} =$ ．

查看试题解析
8. 吉林市北山四季越野滑雪场是亚洲首个具有国际水平，可进行全天候标准化越野滑雪专业训练场地，总投资约为 $990000000$ 元．数字 $990000000$ 用科学记数法表示为．

查看试题解析
9. 某工厂去年的产值是a万元，今年比去年增加10%，今年的产值是万元．

查看试题解析
10. 方程 $\frac{2}{x} = \frac{1}{x - 3}$ 的解为．

查看试题解析
11. 关于 $x$ 的一元二次方程 $x^{2} + x - \frac{k}{4} = 0$ 有两个不相等的实数根，则 $k$ 的值可以（写出一个即可）．

查看试题解析
12. 如图，在 $▱ A B C D$ 中， $A D = 3 ， A B = 5 ， A D ⊥ A C$ ．若 $A B$ 的垂直平分线分别交 $A B ， A C$ 于点 $E ，$ 点 $F$ ，则 $F C + F B =$ ．

查看试题解析
13. 如图，在 $R t △ A B C ， ∠ B = 90 ° ， ∠ A C B = 50 °$ ，将 $R t △ A B C$ 在平面内绕点 $A$ 逆时针旋转到 $△ A B^{'} C^{'}$ 的位置，连接 $C C^{'}$ .若则 $A B // C C^{'} ，$ 旋转角的度数为 $^{\circ}$

查看试题解析
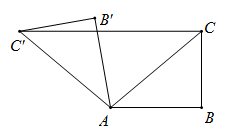14. 图①中特种自行车的轮子形状为“勒络三角形”，图②是其一个轮子的示意图，“勒络三角形”是分别以等边三角形 $A B C$ 三个顶点 $A ， B ， C$ 为圆心，以边长为半径的三段弧围成的图形、若这个等边三角形 $A B C$ 的边长为 $30 c m ，$ 则这种自行车一个轮子的周长为 $c m$ ．

查看试题解析

三、解答题

15. 先化简，再求值： $(a + 3) (a - 3) + 2 (a^{2} + 4) ，$ 其中 $a = \sqrt{3}$ ．

查看试题解析
16. 一个不透明的口袋中有三个小球，颜色分别为红、黄、蓝，除颜色外其余均相同．从口袋中随机摸出一个小球，记下小球颜色后放回并搅匀；再从口袋中随机摸出一个小球记下颜色，用画树状图（或列表）的方法，求两次摸出的小球颜色相同的概率．

查看试题解析
17. 李老师为学校购买口罩，第一次用 $3350$ 元购买医用外科口罩 $1000$ 个， $K N 95$ 型口罩 $50$ 个；第二次用 $5200$ 元购买医用外科口罩 $1500$ 个，KN95型口罩 $100$ 个．若两次购买的同类口罩单价相同，求这两种口罩的单价．

查看试题解析
18. 如图，四边形 $A B C D$ 是正方形，分别以 $B ， C$ 为圆心， $B C$ 长为半径画弧，两弧交于点 $E ，$ 连接 $A E ， B E ， C E ， D E$ ，求证： $△ A B E ≌ △ D C E$ ．

查看试题解析
19. 李老师为了准备网课直播，购买了一个三脚架，如图①所示，图②为其截面示意图.测得 $O C = O D = 60 c m ，$ $A O = 100 c m ，$ $∠ C O B = ∠ D O B = 32^{\circ}$ .求点 $A$ 到地面 $C D$ 的高度（结果精确到 $1 c m$ ）.
（参考数据： $s i n 32 ° \approx 0.53 ， c o s 32 ° \approx 0.85 ， t a n 32 ° \approx 0.62$ .）

查看试题解析
20. 如图，点A（1，6）和点B在反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象上，AD⊥x轴于点D，BC⊥x轴于点C，BE⊥y轴于点E，交AD于点F．

(1)、求反比例函数的解析式；

(2)、若DC＝5，求四边形DFBC的面积．

查看试题解析
21. 图①，图②，图③都是由 $12$ 个全等的小矩形构成的网格，每个小矩形较短的边长为 $1 ，$ 每个小矩形的顶点称为格点.线段 $A B$ 的端点在格点上.

(1)、在图①中画 $∠ A B C = 45^{\circ} ，$ 使点 $C$ 在格点上；

(2)、在图②中以 $A B$ 为边画一个面积为 $5$ 的平行四边形，且另外两个顶点在格点上；

(3)、在图③中以 $A B$ 为边画一个面积最大的平行四边形，且另外两个顶点在格点上.

查看试题解析
22. 为了调查八年级学生网课期间体育锻炼的时间情况，某校在八年级 $350$ 名学生中随机抽取了男生，女生各 $18$ 名，收集得到了以下数据：（单位：分钟）
女生： $28 ， 30 ， 32 ， 46 ， 68 ， 39 ， 80 ， 70 ， 66 ，$ $57 ， 70 ， 95 ， 100 ， 58 ， 69 ， 88 ， 99 ， 105$ ．

男生： $37 ， 48 ， 78 ， 99 ， 56 ， 62 ， 35 ， 109 ， 29$ ， $87 ， 88 ， 69 ， 73 ， 55 ， 90 ， 98 ， 69 ， 72$ ．

整理数据：制作了如下统计表，

分析数据：两组数据的平均数、中位数、众数如表所示，

(1)、请将上面的表格补充完整： $m =$ ， $n =$ ， $a =$ ， $b =$ ；

(2)、若该校学生 $60 %$ 为男生，根据调查的数据，估计八年级居家体育锻炼的时间在 $90$ 分钟以上（不包含 $90$ 分钟）的男生的有多少名？

(3)、体育老师分析表格数据后，认为八年级的男生居家体育锻炼做得比女生好，请你结合统计数据，写出一条同意体育老师观点的理由．

查看试题解析
23. 在抗击“新冠肺炎”疫情期间，需要印刷一批宣传单．某印刷厂由甲、乙两台机器同时印刷，甲机器印刷一段时间后，出现故障，停下来维修，排除故障后继续以原来的速度印刷．两台机器还需印刷总量 $y$ （份）与印刷时间 $x$ （分钟）的函数关系如图所示．

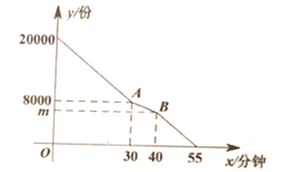(1)、甲机器维修的时间是分钟，甲乙两台机器一分钟共印宣传单份；

(2)、求线段AB的函数解析式，并写出自变量的取值范围；

(3)、若甲机器没有发生故障，可提前多少分钟印刷完这批宣传单．

查看试题解析
24. 在等腰直角三角形纸片ABC中，点D是斜边AB的中点，AB＝10，点E为BC上一点，将纸片沿DE折叠，点B的对应点为点B'．

(1)、如图①，连接CD，求CD的长；

(2)、如图②，B'E与AC交于点F，DB'∥BC．

①求证：四边形BDB'E为菱形；

②连接B'C，判断△B'FC的形状；

(3)、如图③，求△CEF的周长．

查看试题解析
25. 如图，在Rt△ABC中，∠BAC＝90°，∠B＝30°，AD⊥BC于D，AD＝4cm，过点D作DE∥AC，交AB于点E，DF∥AB，交AC于点F．动点P从点A出发以1cm/s的速度向终点D运动，过点P作MN∥BC，交AB于点M，交AC于点N．设点P运动时间为x （s），△AMN与四边形AEDF重叠部分面积为y（cm²）．

(1)、AE＝cm，AF＝cm；

(2)、求y关于x的函数解析式，并写出x的取值范围；

(3)、若线段MN中点为O，当点O落在∠ACB平分线上时，直接写出x的值．

查看试题解析
26. 如图，抛物线y＝ax²+bx+c（a＜0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C，对称轴为直线x＝ $\frac{1}{2}$ ；连接AC，BC，S_△ABC＝15．

(1)、求抛物线的解析式；

(2)、①点M是x轴上方抛物线上一点，且横坐标为m，过点M作MN⊥x轴，垂足为点N．线段MN有一点H（点H与点M，N不重合），且∠HBA+∠MAB＝90°，求HN的长；
②在①的条件下，若MH＝2NH，直接写出m的值；

(3)、在（2）的条件下，设d＝ $\frac{S_{Δ M A N}}{S_{Δ N B H}}$ ，直搂写出d关于m的函数解析式，并写出m的取值范围．

查看试题解析