黑龙江省绥化肇东市2020年中考数学一模试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 4的倒数的相反数是（）

A、﹣4 B、4 C、- $\frac{1}{4}$ D、 $\frac{1}{4}$

查看试题解析
2. 下图中的正五棱柱的左视图应为（）

A、 B、 C、 D、

查看试题解析
3. 使代数式 $\frac{\sqrt{x - 3}}{x - 4}$ 有意义的自变量x的取值范围是（）

A、x≥3 B、x＞3且x≠4 C、x≥3且x≠4 D、x＞3

查看试题解析
4. 某公司今年销售一种产品，一月份获得利润10万元，由于产品畅销，利润逐月增加，一季度共获利36.4万元，已知2月份和3月份利润的月增长率相同．设2，3月份利润的月增长率为x，那么x满足的方程为（）

A、10（1+x）²=36.4 B、10+10（1+x）²=36.4 C、10+10（1+x）+10（1+2x）=36.4 D、10+10（1+x）+10（1+x）²=36.4

查看试题解析
5. 下列命题中，错误的是（）

A、矩形的对角线互相平分且相等 B、对角线互相垂直的四边形是菱形 C、三角形的三条角平分线相交于一点，并且这点到三条边的距离相等 D、到一条线段两个端点距离相等的点在这条线段的垂直平分线上

查看试题解析
6. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△DOE：S_△COA=1：25，则 $\frac{B E}{E C}$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{5}$

查看试题解析

二、填空题

7. 国家体育场“鸟巢”工程总占地面积21公顷，建筑面积258000 m².那么，258000用科学记数法表示为.

查看试题解析
8. 在实数π、 $\sqrt{3}$ 、﹣ $\frac{1}{7}$ 、0.303003…（相邻两个3之间依次多一个0）中，无理数有个

查看试题解析
9. 分解因式：x³y﹣2x²y+xy= ．

查看试题解析
10. 化简； $\frac{x^{2} - 4 x + 4}{x^{2} + 2 x}$ ÷（ $\frac{4}{x + 2}$ ﹣1）= ．

查看试题解析
11. 如图，正方形内的阴影部分是由四个直角边长都是1和3的直角三角形组成的，假设可以在正方形内部随意取点，那么这个点取在阴影部分的概率为．

查看试题解析
12.
如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．

查看试题解析
13. 等腰三角形一腰上的高与另一腰的夹角为 $48^{\circ}$ ，则该等腰三角形的底角的度数为．

查看试题解析
14. 如图，矩形ABCD中，AB=2，BC=3，点E为AD上一点，且∠ABE=30°，将△ABE沿BE翻折，得到△A′BE，连接CA′并延长，与AD相交于点F，则DF的长为．

查看试题解析
15. 如图，已知等边△ $O A_{1} B_{1}$ ，顶点 $A_{1}$ 在双曲线 $y = \frac{\sqrt{3}}{x} (x > 0)$ 上，点 $B_{1}$ 的坐标为 $(2 ， 0)$ ．过 $B_{1}$ 作 $B_{1} A_{2} / / O A_{1}$ 交双曲线于点 $A_{2}$ ，过 $A_{2}$ 作 $A_{2} B_{2} / / A_{1} B_{1}$ 交 $x$ 轴于点 $B_{2}$ ，得到第二个等边△ $B_{1} A_{2} B_{2}$ ；过 $B_{2}$ 作 $B_{2} A_{3} / / B_{1} A_{2}$ 交双曲线于点 $A_{3}$ ，过 $A_{3}$ 作 $A_{3} B_{3} / / A_{2} B_{2}$ 交 $x$ 轴于点 $B_{3}$ ，得到第三个等边△ $B_{2} A_{3} B_{3}$ ；以此类推， $\dots$ ，则点 $B_{6}$ 的坐标为．

查看试题解析

三、解答题

16. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣3，4），B（﹣5，2），C（﹣2，1）.

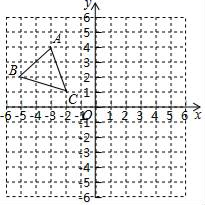(1)、画出△ABC关于y轴的对称图形△A₁B₁C₁；

(2)、画出将△ABC绕原点O逆时针方向旋转90°得到的△A₂B₂C₂；

(3)、求（2）中线段OA扫过的图形面积.

查看试题解析
17. 已知关于 $x$ 的方程 $(k - 1) x^{2} + 2 k x + 2 = 0$

(1)、求证：无论 $k$ 为何值，方程总有实数根.

(2)、设 $x_{1}$ ， $x_{2}$ 是方程 $(k - 1) x^{2} + 2 k x + 2 = 0$ 的两个根，记 $S = \frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} + x_{1} + x_{2}$ ，S的值能为2吗？若能，求出此时 $k$ 的值；若不能，请说明理由.

查看试题解析
18. 如图，已知AB为⊙O的直径，AD ， BD是⊙O的弦，BC是⊙O的切线，切点为B ， OC∥AD ， BA ， CD的延长线相交于点E.

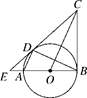(1)、求证：DC是⊙O的切线；

(2)、若AE＝1，ED＝3，求⊙O的半径．

查看试题解析
19. “低碳环保，绿色出行”的理念得到广大群众的接受，越来越多的人喜欢选择自行车作为出行工具 $.$ 小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米 $/$ 分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆，小军始终以同一速度骑行，两人行驶的路程 $y ($ 米 $)$ 与时间 $x ($ 分钟 $)$ 的关系如图，请结合图象，解答下列问题：

(1)、a= ， $b =$ ， $m =$ ；

(2)、若小军的速度是120米 $/$ 分，求小军在途中与爸爸第二次相遇时，距图书馆的距离；

(3)、在 $(2)$ 的条件下，爸爸自第二次出发至到达图书馆前，何时与小军相距100米？

查看试题解析
20. 如图，正方形ABCD的顶点A在等腰直角三角形DFG的斜边FG上，G与BC相交于点E，连接CF．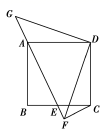

(1)、求证： $△ A D G ≌ △ C D F$ ；

(2)、求证： $△ A B E ∽ △ C F E$ ；

(3)、若正方形ABCD的边长为2，点E是BC的中点，求FG的长．

查看试题解析
21. 二次函数 $y = a x^{2} + b x + c$ 的图象经过点（﹣1，4），且与直线 $y = - \frac{1}{2} x + 1$ 相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）.

(1)、求二次函数的表达式；

(2)、点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；

(3)、在（2）的条件下，点N在何位置时，BM与NC相互垂直平分？并求出所有满足条件的N点的坐标.

查看试题解析