黑龙江省绥化肇东市2020年中考数学三模试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2.
如图是由6个相同的小立方块搭成的几何体，则下列说法正确的是（　　）

A、主视图的面积最大 B、俯视图的面积最大 C、左视图的面积最大 D、三个视图面积一样大

查看试题解析
3. 下列函数中是反比例函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = - \frac{\sqrt{3}}{3 x}$ C、 $y = \frac{2}{x^{2}}$ D、 $y = 1 - \frac{1}{x}$

查看试题解析
4. 将抛物线 $y = x^{2} - 6 x + 5$ 向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）

A、 $y = {(x - 4)}^{2} - 6$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x - 2)}^{2} - 2$ D、 $y = {(x - 4)}^{2} - 2$

查看试题解析
5.
如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（　　）

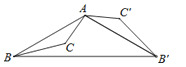A、45° B、60° C、70° D、90°

查看试题解析
6. 将一长为6米的梯子CD斜靠在墙面，梯子与地面所成的角∠BCD=55°，此时梯子的顶端与地面的距离BD的长为（）米．

A、6cos55° B、 $\frac{6}{\sin 55^{\circ}}$ C、6sin55° D、 $\frac{6}{\cos 55^{\circ}}$

查看试题解析
7. 当x=2时，正比例函数y=k₁x（k₁≠0）与反比例函数y= $\frac{k_{2}}{x}$ （k₂≠0）的值相等，则k₁与k₂的比是（）

A、4：1 B、2：1 C、1：2 D、1：4

查看试题解析
8. 为了让市民享受到更多的优惠，相关部门拟确定一个折扣线，计划使 $30 %$ 左右的人获得折扣优惠．某市针对乘坐地铁的人群进行了调查．调查小组在各地铁站随机调查了该市 $1000$ 人上一年乘坐地铁的月均花费（单位：元），绘制了频数分布直方图，如图所示．下列说法正确的是（）

①每人乘坐地铁的月均花费最集中的区域在 $60 - 80$ 元范围内；

②每人乘坐地铁的月均花费的平均数范围是 $40 - 60$ 元范围内；

③每人乘坐地铁的月均花费的中位数在 $100 - 120$ 元范围内；

④乘坐地铁的月均花费达到 $100$ 元以上的人可以享受折扣．

A、①④ B、③④ C、①③ D、①②

查看试题解析
9. 为了估计池塘里有多少条鱼，从池塘里捕捞了1000条鱼做上标记，然后放回池塘里，经过一段时间，等有标记的鱼完全混合于鱼群中以后，再捕捞200条，若其中有标记的鱼有5条，则估计池塘里有鱼（）

A、5000条 B、10000条 C、20000条 D、40000条

查看试题解析
10. 抛物线y=﹣x²+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知，有下列说法：
①抛物线与y轴的交点为（0，6）；
②抛物线的对称轴是x=1；
③抛物线与x轴有两个交点，它们之间的距离是 $\frac{5}{2}$ ；
④在对称轴左侧y随x增大而增大．
其中正确的说法是（）

A、①②③ B、②③④ C、②③ D、①④

查看试题解析

二、填空题

11. 已知太阳的半径约为696000000m，696000000这个数用科学记数法可表示为.

查看试题解析
12. 在函数y= $\frac{\sqrt{x + 1}}{x}$ 中，自变量x的取值范围是 .

查看试题解析
13. 若一元二次方程 $a x^{2} + b x + c = 0$ 中的二次项系数，一次项系数和常数项之和等于零，那么方程必有一个根是．

查看试题解析
14. 同时掷两枚质地均匀的骰子，每枚骰子的六个面上分别刻有1到6的点数，则这两枚骰子向上的一面出现的点数相同的概率为。

查看试题解析
15. 计算： $\frac{a^{2} - 1}{a^{2} + 2 a} \div \frac{a - 1}{a}$ = ．

查看试题解析
16. 分解因式： $m^{2} y^{2} - 9 m^{2}$ = ．

查看试题解析
17. 若圆锥的轴截面是一个边长为4的等边三角形，则这个圆锥的侧面展开后所得到的扇形的圆心角的度数是．

查看试题解析
18. 抛物线 $y = x^{2} + 2 x + c$ 的图象分别与x轴、y轴相交于点A、C，点O为坐标原点．若OA=OC，则点A的坐标为．

查看试题解析
19. 一次函数y＝kx＋b，当3≤x≤4时，3≤y≤6，则 $\frac{b}{k}$ 的值是.

查看试题解析
20. 关于 $x$ 的分式方程 $\frac{x}{x + 1} - \frac{a}{x^{2} - 1} = 1$ 的解为负数，则 $a$ 的取值范围．

查看试题解析
21. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”．如图，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，由图可知，她一共采集到的野果数量为个．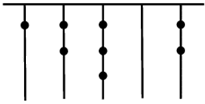

查看试题解析

三、解答题

22. 计算： ${(π - \sqrt{3})}^{0} + {(\frac{1}{2})}^{- 1} - \frac{2}{\sqrt{3} - 1} - \tan 60 ° + \sqrt{12}$

查看试题解析
23. 如图，在平面直角坐标系中，△AOB为直角三角形，点O为坐标原点，顶点A、B的坐标分别为A（0，4），B（-3，0），按要求解答下列问题：

(1)、在平面直角坐标系中，先将Rt△AOB向上平移6个单位，再向右平移3个单位，画出平移后的Rt△A₁O₁B₁；

(2)、在平面直角坐标系中，将Rt△A₁O₁B₁绕点O₁顺时针旋转90°，画出旋转后的Rt△A₂O₁B₂；

(3)、用点A₁旋转到点A₂所经过的路径与O₁A₁、O₁A₂所围成的扇形做一个圆锥的侧面，求这个圆锥的底面周长．（结果保留π）

查看试题解析
24. 如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切.请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．

查看试题解析
25. 已知关于x的方程 $x^{2} - (2 k - 3) x + k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1}$ 、 $x_{2}$ ．

(1)、求 $k$ 的取值范围；

(2)、若抛物线 $y = x^{2} - (2 k - 3) x + k^{2} + 1$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，点 $A$ 、点 $B$ 到原点的距离分别为 $O A$ 、 $O B$ ，且 $O A + O B = 2 O A \cdot O B - 3$ ，求 $k$ 的值．

查看试题解析
26. 如图，⊙O是△ABC的外接圆，AB为直径， OD∥BC交⊙O于点D，交AC于点E，连接AD，BD，CD.

(1)、求证：AD=CD；

(2)、若AB=10，cos∠ABC= $\frac{3}{5}$ ，求tan∠DBC的值.

查看试题解析
27.
现有甲、乙两个容器，分别装有进水管和出水管，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管．直到12分钟时，同时关闭两容器的进出水管．打开和关闭水管的时间忽略不计．容器中的水量y（升）与乙容器注水时间x（分）之间的关系如图所示．

(1)、求甲容器的进、出水速度．

(2)、甲容器进、出水管都关闭后，是否存在两容器的水量相等？若存在，求出此时的时间．

(3)、若使两容器第12分钟时水量相等，则乙容器6分钟后进水速度应变为多少？

查看试题解析
28. 已知正方形ABCD与正方形CEFG，M是AF的中点，连接DM，EM．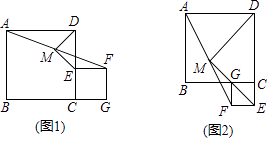

(1)、如图1，点E在CD上，点G在BC的延长线上，请判断DM，EM的数量关系与位置关系，并直接写出结论；

(2)、如图2，点E在DC的延长线上，点G在BC上，（1）中结论是否仍然成立？请证明你的结论；

(3)、将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB=13，CE=5，请画出图形，并直接写出MF的长．

查看试题解析
29. 如图，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与y轴交于点A（0，3），与x轴交于点B（4，0）．

(1)、求抛物线的解析式；

(2)、连接AB，点C为线段AB上的一个动点，过点C作y轴的平行线交抛物线于点D，设C点的横坐标为m，线段CD长度为d（d≠0）．求d与m的函数关系式（不要求写出自变量m的取值范围）；

(3)、在（2）的条件下，连接AD，是否存在m值，使△ACD是等腰三角形？若存在，求出m的值；若不存在，请说明理由．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…