黑龙江省绥化肇东市2020年中考数学二模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 下列各组数中,互为倒数的是( )A、-3 与3 B、-3 与 C、-3与- D、-3 与+(-3)2. 下列图形中,中心对称图形有( )
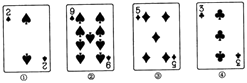 A、1个 B、2个 C、3个 D、4个3. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对的面上的汉字是( )
A、1个 B、2个 C、3个 D、4个3. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对的面上的汉字是( ) A、数 B、活 C、学 D、的4. 下列计算正确的是( )A、x2﹣3x2=﹣2x4 B、(﹣3x2)2=6x2 C、x2y•2x3=2x6y D、6x3y2÷(3x)=2x2y25. 我国研制的“曙光3000超级服务器”排在全世界运算速度最快的500台高性能计算机的第80位,它的峰值速度达到每秒403 200 000 000次,用科学记数法表示它的峰值计算速度为每秒( )次.A、0.4032×1012 B、403.2×109 C、4.032×108 D、4.032×10116. 关于反比例函数y=﹣ 的图象,下列说法正确的是( )A、经过点(﹣1,﹣4) B、当x<0时,图象在第二象限 C、无论x取何值时,y随x的增大而增大 D、图象是轴对称图形,但不是中心对称图形7. 如图,在Rt△ABC中,∠C=90°.D为边CA延长线上的一点,DE∥AB,∠ADE=42°,则∠B的大小为( )
A、数 B、活 C、学 D、的4. 下列计算正确的是( )A、x2﹣3x2=﹣2x4 B、(﹣3x2)2=6x2 C、x2y•2x3=2x6y D、6x3y2÷(3x)=2x2y25. 我国研制的“曙光3000超级服务器”排在全世界运算速度最快的500台高性能计算机的第80位,它的峰值速度达到每秒403 200 000 000次,用科学记数法表示它的峰值计算速度为每秒( )次.A、0.4032×1012 B、403.2×109 C、4.032×108 D、4.032×10116. 关于反比例函数y=﹣ 的图象,下列说法正确的是( )A、经过点(﹣1,﹣4) B、当x<0时,图象在第二象限 C、无论x取何值时,y随x的增大而增大 D、图象是轴对称图形,但不是中心对称图形7. 如图,在Rt△ABC中,∠C=90°.D为边CA延长线上的一点,DE∥AB,∠ADE=42°,则∠B的大小为( ) A、42° B、45° C、48° D、58°8. 某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同.设每次降价的百分率为x,根据题意列方程得( )A、168(1+x)2=108 B、168(1﹣x)2=108 C、168(1﹣2x)=108 D、168(1﹣x2)=1089. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )
A、42° B、45° C、48° D、58°8. 某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同.设每次降价的百分率为x,根据题意列方程得( )A、168(1+x)2=108 B、168(1﹣x)2=108 C、168(1﹣2x)=108 D、168(1﹣x2)=1089. 小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆 的高度与拉绳 的长度相等,小明先将 拉到 的位置,测得 为水平线),测角仪 的高度为 米,则旗杆 的高度为( )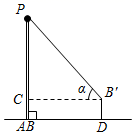 A、 米 B、 米 C、 米 D、 米
A、 米 B、 米 C、 米 D、 米二、填空题
-
10. 若代数式 有意义,则实数x的取值范围是.11. 如图,以点O为位似中心,将△ABC缩小得到△A′B′C,若AA′= 2OA′,则△ABC与△A′B′C′的周长比为.
 12. 一组数据1,2,3,x,5的平均数是3,则该组数据的方差是 .13. 在纸上剪下一个圆和一个扇形纸片,使它们恰好围成一个圆锥(如图所示),如果扇形的圆心角为90°,扇形的半径为4,那么所围成的圆锥的高为.
12. 一组数据1,2,3,x,5的平均数是3,则该组数据的方差是 .13. 在纸上剪下一个圆和一个扇形纸片,使它们恰好围成一个圆锥(如图所示),如果扇形的圆心角为90°,扇形的半径为4,那么所围成的圆锥的高为.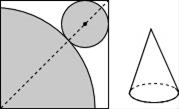 14. 从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是 .
14. 从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是 .
15. 如图,反比例函数 在第一象限内的图象,直线AB//x轴,并分别交两条曲线A、B两点,若S△AOB=2,则k2-k1的值为 .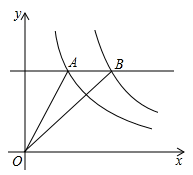 16. 在 中, , ,点D在边AB上,且 ,点E在边AC上,当 时,以A、D、E为顶点的三角形与 相似.
16. 在 中, , ,点D在边AB上,且 ,点E在边AC上,当 时,以A、D、E为顶点的三角形与 相似.
17. 在直角坐标系中,直线l:y= x﹣ 与x轴交于点B1 , 以OB1为边长作等边△A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边△A2A1B2 , 过点A2作A1B2平行于x轴,交直线l于点B3 , 以A2B3为边长作等边△A3A2B3 , …,则等边△A2017A2018B2018的边长是 .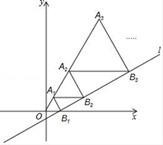
三、解答题
-
18. 计算:|﹣ |+(π﹣2017)°﹣2sin30°+3﹣1 .19. 某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元.一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天共花去住宿费1510元.设该旅游团租住三人间客房 间,两人间客房 间,请列出满足题意的方程组.20. 如图,在正方形网格纸中有一条美丽可爱的小金鱼,其中每个小正方形的边长为1.
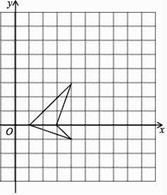 (1)、在同一网格纸中,在y轴的右侧将原小金鱼图案以原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案;(2)、求放大后金鱼的面积.21. 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
(1)、在同一网格纸中,在y轴的右侧将原小金鱼图案以原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案;(2)、求放大后金鱼的面积.21. 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表: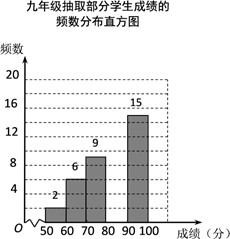

成绩x/分
频数
频率
第1段
x<60
2
0.04
第2段
60≤x<70
6
0.12
第3段
70≤x<80
9
b
第4段
80≤x<90
a
0.36
第5段
90≤x≤100
15
0.30
请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、样本中,部分学生成绩的中位数落在第段;(4)、已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?22. 如图,已知△ABC,∠BAC=90°,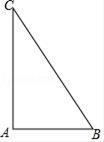 (1)、尺规作图:作∠ABC的平分线交AC于D点(保留作图痕迹,不写作法)(2)、
(1)、尺规作图:作∠ABC的平分线交AC于D点(保留作图痕迹,不写作法)(2)、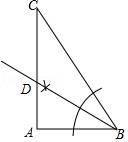 若∠C=30°,求证:DC=DB. 23. 已知关于x的一元二次方程x2+(m+3)x+m+1=0.(1)、求证:无论m取何值,原方程总有两个不相等的实数根;(2)、若x1 , x2是原方程的两根,且 ,求m的值,并求出此时方程的两根.24. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
若∠C=30°,求证:DC=DB. 23. 已知关于x的一元二次方程x2+(m+3)x+m+1=0.(1)、求证:无论m取何值,原方程总有两个不相等的实数根;(2)、若x1 , x2是原方程的两根,且 ,求m的值,并求出此时方程的两根.24. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF. (1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.25. 从甲地到乙地,先是一段平路,然后是一段上坡路.小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.25. 从甲地到乙地,先是一段平路,然后是一段上坡路.小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系. (1)、小明骑车在平路上的速度为km/h;他途中休息了h;(2)、求线段AB,BC所表示的y与 之间的函数关系式;(3)、如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?26. △ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P , 线段EF与射线CA相交于点Q .
(1)、小明骑车在平路上的速度为km/h;他途中休息了h;(2)、求线段AB,BC所表示的y与 之间的函数关系式;(3)、如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?26. △ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P , 线段EF与射线CA相交于点Q .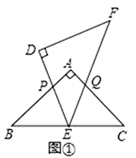
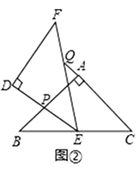 (1)、如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)、如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;(3)、在(2)的条件下,BP=2,CQ=9,则BC的长为 .27. 如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.
(1)、如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)、如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;(3)、在(2)的条件下,BP=2,CQ=9,则BC的长为 .27. 如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C. (1)、求二次函数的解析式;(2)、若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;(3)、若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.
(1)、求二次函数的解析式;(2)、若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;(3)、若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.