黑龙江省齐齐哈尔市甘南县2020年中考数学5月模拟试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. －（－3）²的运算结果是（）

A、6 B、－6 C、9 D、－9

查看试题解析
2. 以下图形中对称轴的数量小于3的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列各式计算正确的是（）

A、a⁰＝1 B、2^﹣2＝﹣ $\frac{1}{4}$ C、a²•a³＝a⁵ D、x²+x²＝x⁴

查看试题解析
4. 小刚参加射击比赛，成绩统计如表，下列说法正确的是（）

成绩（环）

6

7

8

9

10

次数

1

3

2

3

1

A、极差是2环 B、中位数是8环 C、众数是9环 D、平均数是9环

查看试题解析
5. 如图，已知a∥b，直角三角板的直角顶点在直线b上，若∠1=60°，则下列结论错误的是（）

A、∠2=60° B、∠3=60° C、∠4=120° D、∠5=40°

查看试题解析
6. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 3$ ，动点 $P$ 沿折线 $B C D$ 从点 $B$ 开始运动到点 $D$ ．设运动的路程为 $x$ ， $Δ A D P$ 的面积为 $y$ ，那么 $y$ 与 $x$ 之间的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
7. 小明要用40元钱买A、B两种型号的口罩，两种型号的口罩必须都买， 40元钱全部用尽，A型每个6元，B型口罩每个4元，则小明的购买方案有（）种.

A、2种 B、3种 C、4种 D、5种

查看试题解析
8. 用小立方块搭一个几何体，使得它的主视图和俯视图如图所示，则最少需要小立方块的个数为（）

A、6 B、7 C、10 D、13

查看试题解析
9. 如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（）

A、40° B、45° C、50° D、55°

查看试题解析
10. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．其中正确结论的有（）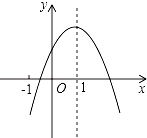

A、①②③ B、①③④ C、③④⑤ D、②③⑤

查看试题解析
11. 如图，在平面直角坐标系中，矩形ABCD的顶点A点，D点分别在x轴、y轴上，对角线BD∥x轴，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过矩形对角线的交点E，若点A(2，0)，D(0，4)，则k的值为（）

A、16 B、20 C、32 D、40

查看试题解析

二、填空题

12. 2020年5月22日，国务院总理李克强对外宣布，国内生产总值首次登上991000亿元的新台阶，把991000用科学记数法表示为．

查看试题解析
13. 在函数y＝ $\frac{1}{\sqrt{x - 3}}$ +（x﹣4）⁰中，自变量x的取值范围是．

查看试题解析
14. 已知圆锥的侧面积是3π，母线是3，则圆锥的高为．

查看试题解析
15. 已知关于 x 的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 的解是非负数，
则 m 的取值范围是.

查看试题解析
16. 已知Rt△ABC中，∠C=90°，AC=6，BC=8，将它的一个锐角翻折，使该锐角顶点落在其对边的中点D处，折痕交另一直角边于E，交斜边于F，则tan∠CDE的值为.

查看试题解析
17. 如图，在平面直角坐标系中，点A₁的坐标为（1，0），以OA₁为直角边作Rt△OA₁A₂ ，并使∠A₁OA₂=60°，再以OA₂为直角边作Rt△OA₂A₃ ，并使∠A₂OA₃=60°，再以OA₃为直角边作Rt△OA₃A₄ ，并使∠A₃OA₄=60°…按此规律进行下去，则点A₂₀₂₀的坐标为．

查看试题解析

三、解答题

18.

(1)、计算： $\sqrt{12}$ +| $\sqrt{3}$ ﹣3|﹣2sin60°﹣（ $\sqrt{3}$ ）²+2016⁰；

(2)、因式分解：1﹣x²+2xy﹣y² ．

查看试题解析
19. 解方程：（2x﹣1）（x+1）＝（3x+1）（x+1）．

查看试题解析
20. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

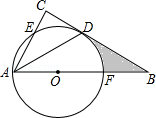(1)、试判断直线BC与⊙O的位置关系，并说明理由；

(2)、若BD=2 $\sqrt{3}$ ，BF=2，求阴影部分的面积（结果保留π）．

查看试题解析

21. 国务院办公厅发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表，请根据所给信息，解答下列问题：

(1)、a＝， b＝，且补全频数分布直方图；

(2)、若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？

(3)、在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．

获奖等次	频数	频率
一等奖	10	0.06
二等奖	20	0.10
三等奖	30	b
优等奖	a	0.30
鼓励奖	80	0.40

查看试题解析

22. 在一条笔直的公路上有A，B，C三地，C地位于A，B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车与C地的距离y₁（单位：km），y₂（单位：km）与甲车行驶时间t（单位：h）之间的函数关系如图．请根据所给图象解答下列问题：

(1)、求甲、乙两车的行驶速度；

(2)、求乙车与C地的距离y₂与甲车行驶时间t之间的函数关系式；

(3)、求乙车出发多少小时，两车相遇？

查看试题解析
23. 已知 $Δ A B C$ 是边长为4的等边三角形，点D是射线BC上的动点，将AD绕点A逆时针方向旋转 $60^{\circ}$ 得到AE，连接DE．

(1)、.如图，猜想 $Δ A D E$ 是三角形；（直接写出结果）

(2)、.如图，猜想线段CA、CE、CD之间的数量关系，并证明你的结论；

(3)、.①当BD等于多少时， $∠ D E C = 30^{\circ}$ ；
②点D在运动过程中， $Δ D E C$ 的周长是否存在最小值？若存在．请直接写出 $Δ D E C$ 周长的最小值；若不存在，请说明理由．

查看试题解析
24. 如图，抛物线y＝﹣x²﹣2x+c的经过D（﹣2，3），与x轴交于A、B两点（点A在点B的左侧）、与y轴交于点C.

(1)、求抛物线的表达式和A、B两点坐标；

(2)、在抛物线的对称轴上有一点P，使得∠OAP＝∠BCO，求点P的坐标；

(3)、点M在抛物线上，点N在抛物线对称轴上.
①当∠ACM＝90°时，求点M的坐标；

②是否存在这样的点M与点N，使以M、N、A、C为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析

成绩（环）	6	7	8	9	10
次数	1	3	2	3	1