黑龙江省哈尔滨市平房区2020年中考数学一模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. ﹣ 的倒数是( )A、﹣ B、 C、﹣ D、2. 下列运算中,结果正确的是( )A、 B、 C、 D、3. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若反比例函数 的图像经过点(3,-2),则k的值为( ).A、-6 B、3 C、6 D、-35. 下面两幅图是由5个小正方体搭成的几何体的主视图与俯视图,则搭成这个几何体的左视图为( )
4. 若反比例函数 的图像经过点(3,-2),则k的值为( ).A、-6 B、3 C、6 D、-35. 下面两幅图是由5个小正方体搭成的几何体的主视图与俯视图,则搭成这个几何体的左视图为( )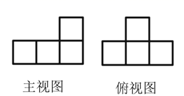 A、
A、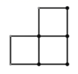 B、
B、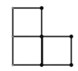 C、
C、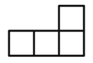 D、
D、 6. 分式方程 的解为( ).A、 B、 C、 D、7. 在 中, , ,若 ,则 的长为( ).A、 B、 C、 D、8. 如图, 为 的直径, 为弦, ,垂足为E,若 ,则 的度数为( ).
6. 分式方程 的解为( ).A、 B、 C、 D、7. 在 中, , ,若 ,则 的长为( ).A、 B、 C、 D、8. 如图, 为 的直径, 为弦, ,垂足为E,若 ,则 的度数为( ). A、135° B、120° C、150° D、110°9. 已知二次函数 向左平移h个单位,再向下平移k个单位,得到二次函数 ,则h和k的值分别为( )A、1,3 B、3,-4 C、1,-3 D、3,-310. 如图,在矩形ABCD中,点F在AD上,射线BF交AC于点G,交CD的延长线于点E,则下列等式正确的为( )
A、135° B、120° C、150° D、110°9. 已知二次函数 向左平移h个单位,再向下平移k个单位,得到二次函数 ,则h和k的值分别为( )A、1,3 B、3,-4 C、1,-3 D、3,-310. 如图,在矩形ABCD中,点F在AD上,射线BF交AC于点G,交CD的延长线于点E,则下列等式正确的为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数2020000用科学记数法表示为 .12. 计算 的结果是 .13. 函数 的自变量x的取值范围是 .14. 把多项式 分解因式的结果是 .15. 不等式组的解集为 的解集为 .16. 如图, , ,若 ,则图中阴影部分的面积为 .
 17. 为了防控新型冠状病毒感染,我区要从3名男士和2名女士中随机抽取2人做宣传活动,抽取的恰好是一名男士和一名女士的概率为 .18. 在“红旗 ”举行的促销活动中,某商品连续两次降价后,售价变为原来的 .若两次降价的百分率相同,则该商品每次降价的百分率为 .19. 在矩形 中,点E是直线 上一点,若 , , ,则 的长为 .20. 如图,在正方形 中,点E为正方形内部一点,连接 、 、 ,若 , , ,则 的长为 .
17. 为了防控新型冠状病毒感染,我区要从3名男士和2名女士中随机抽取2人做宣传活动,抽取的恰好是一名男士和一名女士的概率为 .18. 在“红旗 ”举行的促销活动中,某商品连续两次降价后,售价变为原来的 .若两次降价的百分率相同,则该商品每次降价的百分率为 .19. 在矩形 中,点E是直线 上一点,若 , , ,则 的长为 .20. 如图,在正方形 中,点E为正方形内部一点,连接 、 、 ,若 , , ,则 的长为 .
三、解答题
-
21. 先化简,再求代数式 的值,其中 .22. 如图,方格纸中每个小正方形的边长均为1,线段 、 的端点A、B、D、E均在小正方形的顶点上.
 (1)、在图中画一个以 为斜边的直角三角形 ,且 ,点C在小正方形的顶点上;(2)、在图中画一个以 为腰的等腰三角形 ,且三角形 的面积等于 ,点F在小正方形的顶点上.连接 ,请直接写出线段 的长.23. 为增强学生体质,某中学将在复学后开展体育大课间活动,并通过微信小程序“问卷星”开展以“我最想参加的课间活动”为主题的网络调查活动,围绕“跳绳、踢毽子、打羽毛球、打篮球、踢足球共五种活动中,你最想参加的活动是哪种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行网络问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据统计图的信息回答下列问题:
(1)、在图中画一个以 为斜边的直角三角形 ,且 ,点C在小正方形的顶点上;(2)、在图中画一个以 为腰的等腰三角形 ,且三角形 的面积等于 ,点F在小正方形的顶点上.连接 ,请直接写出线段 的长.23. 为增强学生体质,某中学将在复学后开展体育大课间活动,并通过微信小程序“问卷星”开展以“我最想参加的课间活动”为主题的网络调查活动,围绕“跳绳、踢毽子、打羽毛球、打篮球、踢足球共五种活动中,你最想参加的活动是哪种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行网络问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据统计图的信息回答下列问题: (1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若该中学共有2100名学生,请你估计该中学复学后大课间想参加打篮球的学生大约有多少名.24. 已知:在菱形 中, ,点E和点F分别在 边和 边上,连接 、 、 , .
(1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若该中学共有2100名学生,请你估计该中学复学后大课间想参加打篮球的学生大约有多少名.24. 已知:在菱形 中, ,点E和点F分别在 边和 边上,连接 、 、 , . (1)、如图1,求证: ;(2)、如图2,当点E是 边中点时,连接对角线 分别交 、 、 于点M、O、N,连接 交对角线 于点P,在不添加任何辅助线和字母的情况下,请直接写出图2中面积等于 面积3倍的三角形或四边形.25. 2020年初武汉爆发新冠肺炎疫情,使得口罩成为人们生活的必需品.爱民药店库存一批N95和普通医用两种类型口罩,N95口罩进价是普通医用口罩进价的5倍,药店把N95口罩和普通医用口罩在进价基础上分别加价40%、50%做为零售价.某人在爱民药店用84元购买一种口罩,发现买普通医用口罩的数量恰好比买N95口罩的数量4倍还多4个.(1)、求两种口罩的进价分别是多少元?(2)、随着疫情的进一步恶化,爱民药店的口罩很快被抢购一空.该药店再去厂家进货时发现,由于原材料上涨,N95口罩进价上涨20%,普通医用口罩进价上涨了30%.爱民药店购进这两种口罩共1500个,在零售时,N95口罩保持原售价不变,而普通医用口罩在原售价基础上上调20%,该药店要想在这批口罩全部售出后的利润不少于2000元(不考虑其它因素),则这次至少购进N95口罩多少个?26. 已知: 内接于 ,点D在 上,连接 、 , .
(1)、如图1,求证: ;(2)、如图2,当点E是 边中点时,连接对角线 分别交 、 、 于点M、O、N,连接 交对角线 于点P,在不添加任何辅助线和字母的情况下,请直接写出图2中面积等于 面积3倍的三角形或四边形.25. 2020年初武汉爆发新冠肺炎疫情,使得口罩成为人们生活的必需品.爱民药店库存一批N95和普通医用两种类型口罩,N95口罩进价是普通医用口罩进价的5倍,药店把N95口罩和普通医用口罩在进价基础上分别加价40%、50%做为零售价.某人在爱民药店用84元购买一种口罩,发现买普通医用口罩的数量恰好比买N95口罩的数量4倍还多4个.(1)、求两种口罩的进价分别是多少元?(2)、随着疫情的进一步恶化,爱民药店的口罩很快被抢购一空.该药店再去厂家进货时发现,由于原材料上涨,N95口罩进价上涨20%,普通医用口罩进价上涨了30%.爱民药店购进这两种口罩共1500个,在零售时,N95口罩保持原售价不变,而普通医用口罩在原售价基础上上调20%,该药店要想在这批口罩全部售出后的利润不少于2000元(不考虑其它因素),则这次至少购进N95口罩多少个?26. 已知: 内接于 ,点D在 上,连接 、 , . (1)、如图1,求证: ;(2)、如图2,点E在 上,连接 ,若 ,求证: ;(3)、如图3.在(2)的条件下,若 , , ,求线段 的长.27. 在平面直角坐标系 中,直线 交x轴于点 ,交y轴于点 .
(1)、如图1,求证: ;(2)、如图2,点E在 上,连接 ,若 ,求证: ;(3)、如图3.在(2)的条件下,若 , , ,求线段 的长.27. 在平面直角坐标系 中,直线 交x轴于点 ,交y轴于点 .
 (1)、如图1,求直线 的解析式:(2)、如图2,点E、C分别在 、 上,连接 ,过点O作 交 点D,且 ,连接 ,设点D的横坐标为t, 的面积为S,求S与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,延长 交x轴负半轴于点H,点N、G分别为 、 上的点,连接 ,过点N作直线 ,交 于点M,分别过点F、N作 的垂线,垂足分别为T、Q, , 与 交于点R, ,连接 、 ,当 , 时,求直线 的解析式.
(1)、如图1,求直线 的解析式:(2)、如图2,点E、C分别在 、 上,连接 ,过点O作 交 点D,且 ,连接 ,设点D的横坐标为t, 的面积为S,求S与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,延长 交x轴负半轴于点H,点N、G分别为 、 上的点,连接 ,过点N作直线 ,交 于点M,分别过点F、N作 的垂线,垂足分别为T、Q, , 与 交于点R, ,连接 、 ,当 , 时,求直线 的解析式.