广东省江门市开平市2020年中考数学二模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. ﹣2的绝对值是( )A、2 B、 C、 D、13. 如图是由6个大小相同的小正方体摆成的立体图形,它的主视图是( )
 A、
A、 B、
B、 C、
C、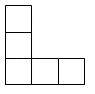 D、
D、 4. 数据1、6、8、3、9的中位数是( )A、3 B、5 C、8 D、65. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
4. 数据1、6、8、3、9的中位数是( )A、3 B、5 C、8 D、65. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 关于x的不等式3x-2≥2x+1的解集是( )A、x≤3 B、x<-3 C、x≥-3 D、x≥37. 如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=1.5,BC=2,则cosB的值是( )
6. 关于x的不等式3x-2≥2x+1的解集是( )A、x≤3 B、x<-3 C、x≥-3 D、x≥37. 如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=1.5,BC=2,则cosB的值是( )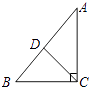 A、 B、 C、 D、8. 下列说法正确的是( )A、可能性很大的事件是必然发生的 B、南方的冬天永远不会下雪 C、工厂生产的产品可能有不合格的 D、掷一枚硬币,正面朝上的概率是9. 已知关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、m> B、m≥ C、m> 且m≠2 D、m≥ 且m≠210. 把函数 与 的图象画在同一个直角坐标系中,正确的是( )A、
A、 B、 C、 D、8. 下列说法正确的是( )A、可能性很大的事件是必然发生的 B、南方的冬天永远不会下雪 C、工厂生产的产品可能有不合格的 D、掷一枚硬币,正面朝上的概率是9. 已知关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、m> B、m≥ C、m> 且m≠2 D、m≥ 且m≠210. 把函数 与 的图象画在同一个直角坐标系中,正确的是( )A、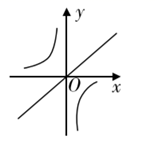 B、
B、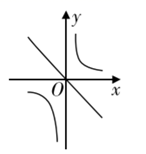 C、
C、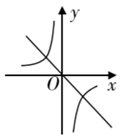 D、
D、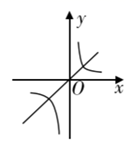
二、填空题
-
11. 因式分解:x3﹣4x= .
12. 一个扇形的半径为 ,面积为 ,则此扇形的圆心角为 .13. 2019年央视春晚创下了跨媒体收视传播新纪录.据统计,除夕当晚,海内外收视的观众总规模达11.73亿人.数据11.73亿人用科学记数法表示为人.14. 两圆的半径分别是x2﹣5x+6=0的两根,圆心距是6,则这两圆的位置关系是 .15. 在一个不透明的袋子中装有除颜色外其他均相同的 个红球, 个黑球,要使从中随机摸取 个球是黑球的概率为 ,则要往袋中添加黑球个16. 不等式3x﹣4≥4+2(x﹣2)的最小整数解是 .17. 若 ,则 的值为 .三、解答题
-
18. 计算: ﹣2sin60°+(﹣1)0+( )﹣2 .19. 先化简,再求值:b(b﹣2a)﹣(a﹣b)2 , 其中a=﹣3,b=﹣ .20. 如图,请用尺规作图法,作出△ABC的BC边上的中线(不要求写作法,保留作图痕迹).
 21. 列方程解应用题:
21. 列方程解应用题:小明和小刚约定周末到某体育公园打羽毛球.他们两家到体育公园的距离分别是1200米,3000米,小刚骑自行车的速度是小明步行速度的3倍,若二人同时到达,则小明需提前4分钟出发,求小明和小刚两人的速度.
22. 某校设有体育选修课,每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中选择一项且只能选择一项球类运动,在该校学生中随机抽取10%的学生进行调查,根据调查结果绘制成如图所示的尚不完整的频数分布表和扇形统计图.运动项目
频数
羽毛球
30
篮球
a
乒乓球
36
排球
b
足球
12

请根据以上图、表信息解答下列问题:
(1)、频数分布表中的a= , b=;(2)、补全扇形统计图;(3)、排球所在的扇形的圆心角为度;(4)、全校有多少名学生选择参加乒乓球运动?23. 如图,小山上有一座120m高的电视发射塔AB,为了测量小山的高度BC,在山脚某处D测得山顶的仰角为22°,测得塔项的仰角为45°.求小山的高.(已知:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)(结果精确到0.1m)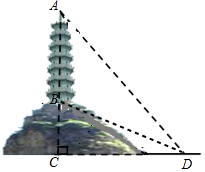 24. 已知:如图一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
24. 已知:如图一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)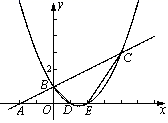 (1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.25. 如图,有一块三角形土地,它的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面积是矩形DEFG的大楼.
(1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.25. 如图,有一块三角形土地,它的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面积是矩形DEFG的大楼. (1)、求地基的面积y(m2)和边EF的长x(m)的函数关系式;(2)、当地基的边长EF为多少时地基的面积最大,最大面积是多少?
(1)、求地基的面积y(m2)和边EF的长x(m)的函数关系式;(2)、当地基的边长EF为多少时地基的面积最大,最大面积是多少?