2016年四川省泸州市中考数学试卷
试卷更新日期:2016-07-22 类型:中考真卷
一、选择题
-
1. 6的相反数为( )A、﹣6 B、6 C、﹣ D、
-
2. 计算3a2﹣a2的结果是( )
A、4a2 B、3a2 C、2a2 D、3 -
3. 下列图形中不是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、
-
4. 将5570000用科学记数法表示正确的是( )A、5.57×105 B、5.57×106 C、5.57×107 D、5.57×108
-
5. 下列立体图形中,主视图是三角形的是( )A、
 B、
B、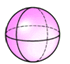 C、
C、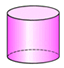 D、
D、
-
6. 数据4,8,4,6,3的众数和平均数分别是( )
A、5,4 B、8,5 C、6,5 D、4,5 -
7. 在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )
A、 B、 C、 D、 -
8.
如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
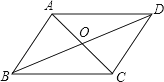 A、10 B、14 C、20 D、22
A、10 B、14 C、20 D、22 -
9. 若关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有实数根,则k的取值范围是( )A、k≥1 B、k>1 C、k<1 D、k≤1
-
10. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A、 B、 C、 D、
-
11.
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()
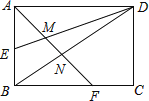 A、 B、 C、 D、
A、 B、 C、 D、 -
12. 已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )A、或1 B、或1 C、或 D、或
二、填空题
-
13. 分式方程 =0的根是 .
-
14. 分解因式:2a2+4a+2= .
-
15. 若二次函数y=2x2﹣4x﹣1的图象与x轴交于A(x1 , 0)、B(x2 , 0)两点,则 的值为 .
-
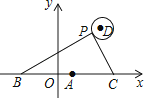
16.
如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
三、本大题共3小题
-
17. 计算:( ﹣1)0﹣ ×sin60°+(﹣2)2 .
-
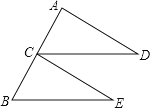
18.
如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
-
19. 化简:(a+1﹣ )• .
四、本大题共2小题
-
20.
为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
节目类型
新闻
体育
动画
娱乐
戏曲
人数
36
90
a
b
27
根据表、图提供的信息,解决以下问题:
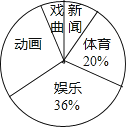 (1)、计算出表中a、b的值;(2)、求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;(3)、若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
(1)、计算出表中a、b的值;(2)、求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;(3)、若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人? -
21. 某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.(1)、A、B两种商品的单价分别是多少元?(2)、已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
五、本大题共2小题
-
22.
如图,为了测量出楼房AC的高度,从距离楼底C处60 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ,计算结果用根号表示,不取近似值).
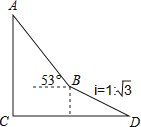
-
23.
如图,一次函数y=kx+b(k<0)与反比例函数y= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
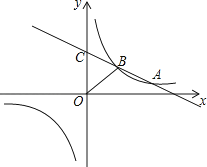 (1)、求反比例函数的解析式;(2)、连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
(1)、求反比例函数的解析式;(2)、连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
六、本大题共2小题
-
24.
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
 (1)、求证:BE是⊙O的切线;(2)、已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG= ,DF=2BF,求AH的值.
(1)、求证:BE是⊙O的切线;(2)、已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG= ,DF=2BF,求AH的值. -
25.
如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
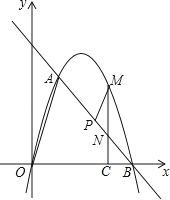 (1)、求出抛物线的解析式;(2)、在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)、点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 的值,并求出此时点M的坐标.
(1)、求出抛物线的解析式;(2)、在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)、点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 的值,并求出此时点M的坐标.
