2017-2018学年北师大版九年级上学期数学期中模拟卷

试卷更新日期：2017-10-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列关于矩形的说法，正确的是（）

A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线相等且互相平分 D、矩形的对角线互相垂直且平分

查看试题解析
2. 一元二次方程 $x^{2} － k x － 1 ＝ 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
3. 方程2（2x+1）（x﹣3）=0的两根分别为（）

A、 $\frac{1}{2}$ 和3 B、﹣ $\frac{1}{2}$ 和3 C、 $\frac{1}{2}$ 和﹣3 D、﹣ $\frac{1}{2}$ 和﹣3

查看试题解析
4. 下列性质中菱形不一定具有的性质是（）

A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形

查看试题解析
5. 下列命题中：
①两条对角线互相平分且相等的四边形是正方形；
②菱形的一条对角线平分一组对角；
③顺次连结四边形各边中点所得的四边形是平行四边形；
④两条对角线互相平分的四边形是矩形；
⑤平行四边形对角线相等．
真命题的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 一个不透明的布袋里装有5个红球、2个白球、3个黄球，它们除颜色外其余都相同．从袋中任意找出1个球，是黄球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{5}$ C、 $\frac{3}{10}$ D、 $\frac{7}{10}$

查看试题解析
7. 若x₁ ， x₂是方程x²﹣2mx+m²﹣m﹣1=0的两个根，且x₁+x₂=1﹣x₁x₂ ，则m的值为（）

A、﹣1或2 B、1或﹣2 C、﹣2 D、1

查看试题解析
8. 盒子中有白色乒乓球8个和黄色乒乓球若干个，为求得盒中黄色乒乓球的个数，某同学进行了如下实验：每次摸出一个乒乓球记下它的颜色，如此重复360次，摸出白色乒乓球90次，则黄色乒乓球的个数估计为（）

A、90个 B、24个 C、70个 D、32个

查看试题解析
9. 为了庆祝教师节，市教育工会组织篮球比赛，赛制为单循环比赛（即每两个队比赛一场）共进行了45场比赛，则这次参加比赛的球队个数为（）

A、8 B、9 C、10 D、11

查看试题解析
10. 如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S_△_ABF=S_△_ADF；②S_△_CDF=4S_△_CEF；③S_△_ADF=2S_△_CEF；④S_△_ADF=2S_△_CDF ，其中正确的是（）

A、①③ B、②③ C、①④ D、②④

查看试题解析

二、填空题

11.
如图，四边形ABCD的对角线互相平分，若再补充一个条件能使四边形ABCD成为矩形，则这个条件是（只填一个条件即可）

查看试题解析
12. 如果关于x的方程x²+2（a+1）x+2a+1=0有一个小于1的正数根，那么实数a的取值范围是．

查看试题解析
13. 如图，在菱形ABCD中，若AC=6，BD=8，则菱形ABCD的面积是．

查看试题解析
14. 正方形ABCD的边长为8，点E为正方形边上一点，连接BE，且BE=10，则AE的长为．

查看试题解析
15. 已知一元二次方程2x²﹣3x﹣1=0的两根为x₁ ， x₂ ，则x₁•x₂= ．

查看试题解析
16. 如图，在矩形ABCD中，AB= $\sqrt{2}$ ，E是BC的中点，AE⊥BD于点F，则CF的长是．

查看试题解析
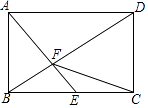17. 甲、乙两位同学各抛掷一枚质地均匀的骰子，他们抛掷的点数分别记为a、b，则a+b=9的概率为．

查看试题解析
18.
如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们面积之和为60米² ，两块绿地之间及周边留有宽度相等的人行通道，则人行道的宽度为米．

查看试题解析

三、解答题

19. 用适当的方法解下列方程：

(1)、3x²+4x﹣7=0；

(2)、3（x﹣2）²=x（x﹣2）

查看试题解析
20. 甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给其余两人的机会是均等的，由甲开始传球，共传三次．

(1)、求三次传球后，球回到甲脚下的概率；

(2)、三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？

查看试题解析
21. 东坡某烘焙店生产的蛋糕礼盒分为六个档次，第一档次（即最低档次）的产品每天生产76件，每件利润10元．调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元．

(1)、若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；

(2)、由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

查看试题解析
22. 甲、乙、丙、丁四人参加某校招聘教师考试，试后甲、乙两人去询问成绩．请你根据下面回答者对甲、乙两人回答的内容进行分析，

(1)、列举出这四人的名次排列所有可能出现的不同情况．

(2)、求甲排在第一名的概率？

查看试题解析
23.
邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，▱ABCD中，若AB=1，BC=2，则▱ABCD为1阶准菱形．

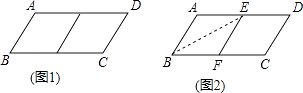(1)、猜想与计算：
邻边长分别为3和5的平行四边形是阶准菱形；已知▱ABCD的邻边长分别为a，b（a＞b），满足a=8b+r，b=5r，请写出▱ABCD是阶准菱形．

(2)、操作与推理：
小明为了剪去一个菱形，进行了如下操作：如图2，把▱ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F处，得到四边形ABFE．请证明四边形ABFE是菱形．

查看试题解析