2016年湖南省永州市中考数学试卷
试卷更新日期：2016-07-22 类型：中考真卷
一、选择题：
-
1. ﹣ 的相反数的倒数是（ ）A、1 B、﹣1 C、2016 D、﹣20162. 不等式组 的解集在数轴上表示正确的是（ ）
A、
B、
C、
D、
3. 下列图案中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
4. 下列运算正确的是（ ）
A、﹣a•a3=a3 B、﹣（a2）2=a4 C、x﹣ x= D、（ ﹣2）（ +2）=﹣15.如图，将两个形状和大小都相同的杯子叠放在一起，则该实物图的主视图为（ ）
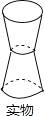A、
B、
C、
D、
6. 在“爱我永州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：甲：8、7、9、8、8
乙：7、9、6、9、9
则下列说法中错误的是（ ）
A、甲、乙得分的平均数都是8 B、甲得分的众数是8，乙得分的众数是9 C、甲得分的中位数是9，乙得分的中位数是6 D、甲得分的方差比乙得分的方差小7. 对下列生活现象的解释其数学原理运用错误的是（ ）A、把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 B、木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理 C、将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 D、将车轮设计为圆形是运用了“圆的旋转对称性”的原理8. 抛物线y=x2+2x+m﹣1与x轴有两个不同的交点，则m的取值范围是（ ）A、m＜2 B、m＞2 C、0＜m≤2 D、m＜﹣29.如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）
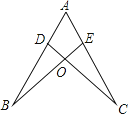A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD10.圆桌面（桌面中间有一个直径为0.4m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为1.2m，桌面离地面1m，若灯泡离地面3m，则地面圆环形阴影的面积是（ ）
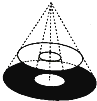A、0.324πm2 B、0.288πm2 C、1.08πm2 D、0.72πm211. 下列式子错误的是（ ）A、cos40°=sin50° B、tan15°•tan75°=1 C、sin225°+cos225°=1 D、sin60°=2sin30°12. 我们根据指数运算，得出了一种新的运算，如表是两种运算对应关系的一组实例：指数运算
21=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
根据上表规律，某同学写出了三个式子：①log216=4，②log525=5，③log2 =﹣1．其中正确的是（ ）
A、①② B、①③ C、②③ D、①②③二、填空题
-
13. 涔天河水库位于永州市江华瑶族自治县境内，其扩建工程是湖南省“十二五”期间水利建设的“一号工程”，也是国务院重点推进的重大工程，其中灌区工程总投资约39亿元．请将3900000000用科学记数法表示为 ．14. 在1，π， ，2，﹣3.2这五个数中随机取出一个数，则取出的这个数大于2的概率是 ．15. 已知反比例函数y= 的图象经过点A（1，﹣2），则k= ．
16. 方程组 的解是 ．
17. 化简： = ．18.如图，在⊙O中，A，B是圆上的两点，已知∠AOB=40°，直径CD∥AB，连接AC，则∠BAC=度．
19. 已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上，且函数值y随x的增大而减小，则k所有可能取得的整数值为 ．
20.如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m=4，由此可知：
①当d=3时，m= ；
②当m=2时，d的取值范围是 ．
三、解答题
-
21. 计算： ﹣（3﹣π）0﹣|﹣3+2|22.
二孩政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度，在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：
(1)、在这次问卷调查中一共抽取了名学生，a=%；(2)、请补全条形统计图；
(3)、持“不赞同”态度的学生人数的百分比所占扇形的圆心角为度；(4)、若该校有3000名学生，请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和．23.如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．
(1)、求证：BE=CD；(2)、连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．24. 某种商品的标价为400元/件，经过两次降价后的价格为324元/件，并且两次降价的百分率相同．
(1)、求该种商品每次降价的百分率；(2)、若该种商品进价为300元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3210元．问第一次降价后至少要售出该种商品多少件？
25.如图，△ABC是⊙O的内接三角形，AB为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE．
(1)、求证：CE是⊙O的切线；(2)、若AC=4，BC=2，求BD和CE的长．26.已知抛物线y=ax2+bx﹣3经过（﹣1，0），（3，0）两点，与y轴交于点C，直线y=kx与抛物线交于A，B两点．
(1)、写出点C的坐标并求出此抛物线的解析式；(2)、当原点O为线段AB的中点时，求k的值及A，B两点的坐标；(3)、是否存在实数k使得△ABC的面积为 ？若存在，求出k的值；若不存在，请说明理由．27.问题探究：
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．
②解决问题
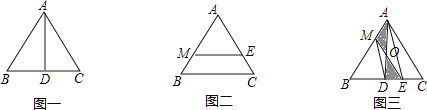
已知等边三角形ABC的边长为2．
(1)、如图一，若AD⊥BC，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；(2)、如图二，若ME∥BC，且ME是△ABC的一条面径，求面径ME的长；(3)、如图三，已知D为BC的中点，连接AD，M为AB上的一点（0＜AM＜1），E是DC上的一点，连接ME，ME与AD交于点O，且S△MOA=S△DOE ．①求证：ME是△ABC的面径；
②连接AE，求证：MD∥AE；
(4)、请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）