2016年湖南省娄底市中考数学试卷
试卷更新日期:2016-07-22 类型:中考真卷
一、选择题
-
1. 2016的相反数是( )A、2016 B、﹣2016 C、 D、﹣2.
已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
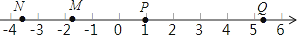 A、M B、N C、P D、Q3. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 下列命题中,错误的是( )A、两组对边分别平行的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、内错角相等5. 下列几何体中,主视图和俯视图都为矩形的是( )A、
A、M B、N C、P D、Q3. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 下列命题中,错误的是( )A、两组对边分别平行的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、内错角相等5. 下列几何体中,主视图和俯视图都为矩形的是( )A、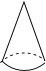 B、
B、 C、
C、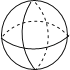 D、
D、 6.
6.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
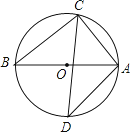 A、20° B、40° C、50° D、70°7. 11名同学参加数学竞赛初赛,他们的等分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
A、20° B、40° C、50° D、70°7. 11名同学参加数学竞赛初赛,他们的等分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
A、平均数 B、中位数 C、众数 D、方差8. 函数y= 的自变量x的取值范围是( )
A、x≥0且x≠2 B、x≥0 C、x≠2 D、x>29. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4 , 乙烷的化学式是C2H6 , 丙烷的化学式是C3H8 , …,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )
A、CnH2n+2 B、CnH2n C、CnH2n﹣2 D、CnHn+310.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
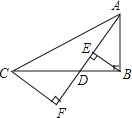 A、不变 B、增大 C、减小 D、先变大再变小
A、不变 B、增大 C、减小 D、先变大再变小二、填空题
-
11. 已知反比例函数y= 的图象经过点A(1,﹣2),则k= .12. 已知某水库容量约为112000立方米,将112000用科学记数法表示为 .13.
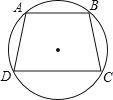
如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是 .
 14.
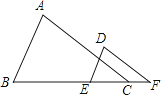
14.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 . (只需写一个条件,不添加辅助线和字母)
 15. 将直线y=2x+1向下平移3个单位长度后所得直线的解析式是 .
15. 将直线y=2x+1向下平移3个单位长度后所得直线的解析式是 .
16. 从“线段,等边三角形,圆,矩形,正六边形”这五个圆形中任取一个,取到既是轴对称图形又是中心对称图形的概率是 .17.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为 .
 18. 当a、b满足条件a>b>0时, =1表示焦点在x轴上的椭圆.若 =1表示焦点在x轴上的椭圆,则m的取值范围是 .
18. 当a、b满足条件a>b>0时, =1表示焦点在x轴上的椭圆.若 =1表示焦点在x轴上的椭圆,则m的取值范围是 .三、解答题
-
19. 计算:(π﹣ )0+| ﹣1|+( )﹣1﹣2sin45°.20. 先化简,再求值:(1﹣ )• ,其中x是从1,2,3中选取的一个合适的数.
四、解答题
-
21.
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
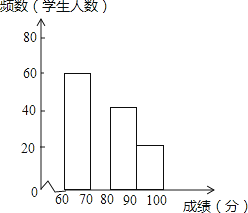 (1)、在表中的频数分布表中,m= , n= .
(1)、在表中的频数分布表中,m= , n= .成绩
频数
频率
60≤x<70
60
0.30
70≤x<80
m
0.40
80≤x<90
40
n
90≤x≤100
20
0.10
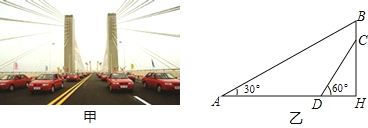
(2)、请补全图中的频数分布直方图.(3)、按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?22.芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ≈1.732)
五、解答题
-
23. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)、求乙骑自行车的速度;(2)、当甲到达学校时,乙同学离学校还有多远?24.
如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
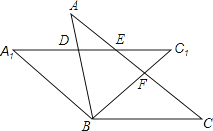 (1)、求证:△BCF≌△BA1D.(2)、当∠C=α度时,判定四边形A1BCE的形状并说明理由.
(1)、求证:△BCF≌△BA1D.(2)、当∠C=α度时,判定四边形A1BCE的形状并说明理由.六、解答题
-
25.
如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
 (1)、求证:∠B=∠ACD.(2)、已知点E在AB上,且BC2=AB•BE.
(1)、求证:∠B=∠ACD.(2)、已知点E在AB上,且BC2=AB•BE.(i)若tan∠ACD= ,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
26.如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
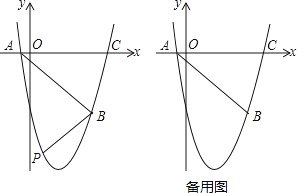 (1)、求抛物线的解析式;(2)、如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
(1)、求抛物线的解析式;(2)、如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.