2016年湖南省常德市中考数学试卷
试卷更新日期:2016-07-22 类型:中考真卷
一、选择题
-
1. 4的平方根是( )
A、2 B、﹣2 C、± D、±22. 下面实数比较大小正确的是( )A、3>7 B、 C、0<﹣2 D、22<33.如图,已知直线a∥b,∠1=100°,则∠2等于( )
 A、80° B、60° C、100° D、70°4.
A、80° B、60° C、100° D、70°4.如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列说法正确的是( )A、袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球 B、天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 C、某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖 D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上6. 若﹣x3ya与xby是同类项,则a+b的值为( )
5. 下列说法正确的是( )A、袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球 B、天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 C、某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖 D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上6. 若﹣x3ya与xby是同类项,则a+b的值为( )
A、2 B、3 C、4 D、57. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( ) A、1 B、2 C、3 D、48. 某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )A、9天 B、11天 C、13天 D、22天
A、1 B、2 C、3 D、48. 某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )A、9天 B、11天 C、13天 D、22天二、填空题
-
9. 使代数式 有意义的x的取值范围是 .
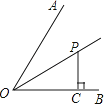
10. 计算:a2•a3= .11.如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为 .
 12. 已知反比例函数y= 的图象在每一个象限内y随x的增大而增大,请写一个符合条件的反比例函数解析式 .
12. 已知反比例函数y= 的图象在每一个象限内y随x的增大而增大,请写一个符合条件的反比例函数解析式 .
13. 张朋将连续10天引体向上的测试成绩(单位:个)记录如下:16,18,18,16,19,19,18,21,18,21.则这组数据的中位数是 .14. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是 .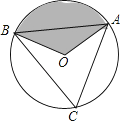 15. 如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1 , 折痕为EF,若∠BAE=55°,则∠D1AD= .
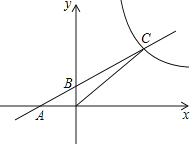
15. 如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1 , 折痕为EF,若∠BAE=55°,则∠D1AD= . 16. 平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
16. 平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
三、计算题
-
17. 计算:﹣14+ sin60°+( )﹣2﹣( )0 .
18. 解不等式组,并把解集在是数轴上表示出来..
四、解答题
-
19. 先化简,再求值:( ) ,其中x=2.20. 如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.
 21. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?22. 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, =1.732, =1.414)
21. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?22. 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, =1.732, =1.414) 23. 今年元月,国内一家网络诈骗举报平台发布了《2015年网络诈骗趋势研究报告》,根据报告提供的数据绘制了如下的两幅统计图:
23. 今年元月,国内一家网络诈骗举报平台发布了《2015年网络诈骗趋势研究报告》,根据报告提供的数据绘制了如下的两幅统计图: (1)、该平台2015年共收到网络诈骗举报多少例?(2)、2015年通过该平台举报的诈骗总金额大约是多少亿元?(保留三个有效数字)(3)、2015年每例诈骗的损失年增长率是多少?(4)、为提高学生的防患意识,现准备从甲、乙、丙、丁四人中随机抽取两人作为受骗演练对象,请用树状图或列表法求恰好选中甲、乙两人的概率是多少?24. 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
(1)、该平台2015年共收到网络诈骗举报多少例?(2)、2015年通过该平台举报的诈骗总金额大约是多少亿元?(保留三个有效数字)(3)、2015年每例诈骗的损失年增长率是多少?(4)、为提高学生的防患意识,现准备从甲、乙、丙、丁四人中随机抽取两人作为受骗演练对象,请用树状图或列表法求恰好选中甲、乙两人的概率是多少?24. 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB. (1)、求证:BE是⊙O的切线;(2)、若BC= ,AC=5,求圆的直径AD及切线BE的长.25. 已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)、求证:BE是⊙O的切线;(2)、若BC= ,AC=5,求圆的直径AD及切线BE的长.25. 已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.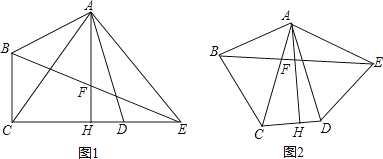 (1)、如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;(2)、如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
(1)、如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;(2)、如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
26. 如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2). (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);(3)、过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.