初中数学华师大版八年级下学期 第19章 19.2 菱形
试卷更新日期:2021-03-19 类型:同步测试
一、单选题
-
1. 矩形具有而菱形不具有的性质是( )A、对边平行且相等 B、对角线垂直 C、对角线互相平分 D、对角线相等2. 已知四边形ABCD是平行四边形,则下列结论中正确的是( )A、当AB⊥BD时,它是菱形 B、当AC=BD时,它是正方形 C、当∠ABC=90°时,它是矩形 D、当AB=BC时,它是矩形3. 如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是( )
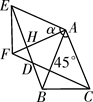
 A、AC⊥BD B、BA⊥BD C、AB=CD D、AD=BC4. 如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:
A、AC⊥BD B、BA⊥BD C、AB=CD D、AD=BC4. 如图,正方形 的边长为1, , 是对角线.将 绕着点 顺时针旋转45°得到 , 交 于点 ,连接 交 于点 ,连接 .则下列结论:①四边形 是菱形 ② ③ ④
其中正确的结论是有( )个
 A、1 B、2 C、3 D、45. 如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=( )
A、1 B、2 C、3 D、45. 如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=( ) A、30° B、70° C、30°或60° D、40°或70°6. 如图,菱形ABCD的对角线AC、BD交于点O , AC=8,BD=6,DE⊥AB于点E , 则DE的长为( )
A、30° B、70° C、30°或60° D、40°或70°6. 如图,菱形ABCD的对角线AC、BD交于点O , AC=8,BD=6,DE⊥AB于点E , 则DE的长为( )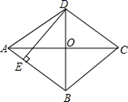 A、4.8 B、5 C、9.6 D、107. 已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )A、4 B、 C、2 D、18. 已知一个菱形的边长是5cm,两条对角线长的比是4:3,则这个菱形的面积是( )A、12cm2 B、24cm2 C、48cm2 D、96cm29. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )
A、4.8 B、5 C、9.6 D、107. 已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )A、4 B、 C、2 D、18. 已知一个菱形的边长是5cm,两条对角线长的比是4:3,则这个菱形的面积是( )A、12cm2 B、24cm2 C、48cm2 D、96cm29. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ) A、1 B、2 C、
A、1 B、2 C、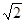 D、
10. 如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为( )
D、
10. 如图,小华剪了两条宽为 的纸条,交叉叠放在一起,且它们较小的交角为 ,则它们重叠部分的面积为( ) A、1 B、2 C、 D、
A、1 B、2 C、 D、二、填空题
-
11. 菱形ABCD中,对角线AC长为10cm,BD=6cm,则菱形ABCD的面积为cm2.12. 菱形有一个内角为120°,较长的对角线长为6 ,则它的面积为.13. 如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
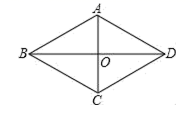 14. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 .
14. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 .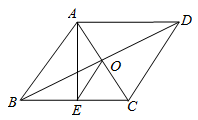
三、综合题
-
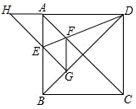
15. 如图,在等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH,

求证:四边形EBFC是菱形.