天津109中2016-2017学年中考数学模拟试卷
试卷更新日期:2017-10-26 类型:中考模拟
一、选择题:
-
1. 计算5﹣(﹣2)×3的结果等于( )A、﹣11 B、﹣1 C、1 D、112. 在Rt△ABC中,∠C=90°,若tanA= ,则sinA=( )
A、 B、 C、 D、3. 点p(5,﹣3)关于原点对称的点的坐标是( )
A、(3,﹣5) B、(﹣5,﹣3) C、(﹣5,3) D、(﹣3,5)4. 如图,几何体是由3个大小完全一样的正方体组成的,它的左视图是( ) A、
A、 B、
B、 C、
C、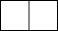 D、
D、 5. 下列运算中,错误的个数为( )
5. 下列运算中,错误的个数为( )① =1 ;② =±4;③ =﹣ ;④ = + = .
A、1 B、2 C、3 D、46. 化简 的结果是( )A、 B、 C、x+1 D、x﹣17. 方程3x(x﹣1)=5(x﹣1)的根为( )A、x= B、x=1 C、x1=1 x2= D、x1=1 x2=8. 要使式子 有意义,则x的取值范围是( )A、x>0 B、x≥﹣2 C、x≥2 D、x≤29. 如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )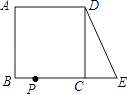 A、3 B、5 C、7 D、3或710. 函数y=﹣ 的图象经过点A(x1 , y1)、B(x2 , y2),若x1<x2<0,则y1、y2、0三者的大小关系是( )A、y1<y2<0 B、y2<y1<0 C、y1>y2>0 D、y2>y1>011. 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
A、3 B、5 C、7 D、3或710. 函数y=﹣ 的图象经过点A(x1 , y1)、B(x2 , y2),若x1<x2<0,则y1、y2、0三者的大小关系是( )A、y1<y2<0 B、y2<y1<0 C、y1>y2>0 D、y2>y1>011. 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )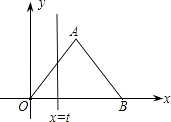 A、
A、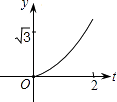 B、
B、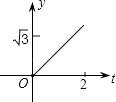 C、
C、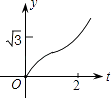 D、
D、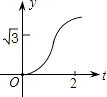
二、填空题:
-
12. 计算:(﹣3x2y)•( xy2)= .13. 计算: ﹣ = .14. 在一个不透明的口袋中,装有若干个除颜色不同外,其余都相同的小球.如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为 ,那么口袋中小球共有个.15. 已知一次函数y=ax+b(a、b为常数),x与y的部分对应值如右表:
x
﹣2
﹣1
0
1
2
3
y
6
4
2
0
﹣2
﹣4
那么方程ax+b=0的解是 , 不等式ax+b>0的解是 .
16. 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 .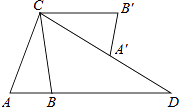 17. 如图,在平面直角坐标系中,抛物线y=a1(x﹣2)2+2与y=a2(x﹣2)2﹣3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(﹣1,0),则△ADE与△BOC的面积比为 .
17. 如图,在平面直角坐标系中,抛物线y=a1(x﹣2)2+2与y=a2(x﹣2)2﹣3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(﹣1,0),则△ADE与△BOC的面积比为 .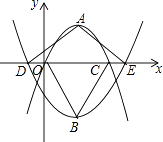
三、简答题:
-
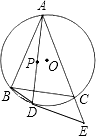
18. 解不等式组: ,并把解集在数轴上表示出来.19. 已知甲同学手中藏有三张分别标有数字 、 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.(1)、请你用树形图或列表法列出所有可能的结果;(2)、现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.20. 如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB•AE.
求证:DE是⊙O的切线.
 21. 已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE= ,cos∠ACD= ,求tan∠AEC的值及CD的长.
21. 已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE= ,cos∠ACD= ,求tan∠AEC的值及CD的长.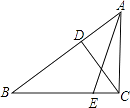 22. 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
22. 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.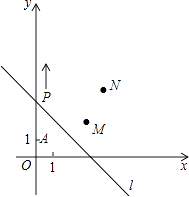 (1)、当t=2时,则AP= , 此时点P的坐标是 .(2)、当t=3时,求过点P的直线l:y=﹣x+b的解析式?(3)、当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?(4)、点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .23. 如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)、当t=2时,则AP= , 此时点P的坐标是 .(2)、当t=3时,求过点P的直线l:y=﹣x+b的解析式?(3)、当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?(4)、点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .23. 如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.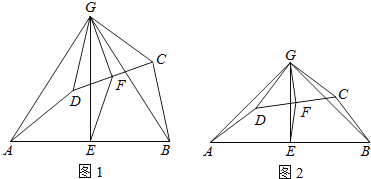 (1)、求证:AD=BC;(2)、求证:△AGD∽△EGF;(3)、如图2,若AD、BC所在直线互相垂直,求 的值.24. 如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
(1)、求证:AD=BC;(2)、求证:△AGD∽△EGF;(3)、如图2,若AD、BC所在直线互相垂直,求 的值.24. 如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.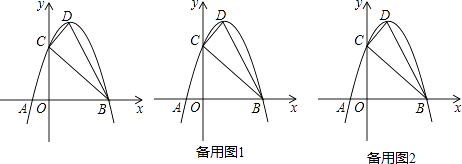 (1)、填空:点C的坐标为( , ),点D的坐标为( , );(2)、设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;(3)、在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
(1)、填空:点C的坐标为( , ),点D的坐标为( , );(2)、设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;(3)、在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?