湖北省武汉二十七中2016-2017学年中考数学模拟试卷

试卷更新日期：2017-10-26 类型：中考模拟

进入出卷网下载

一、选择题：

1. 2的绝对值是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各数：（﹣3）² ， 0，﹣（﹣ $\frac{1}{2}$ ）² ， $\frac{22}{7}$ ，（﹣1）²⁰⁰⁹ ， ﹣2² ， ﹣（﹣8），﹣|﹣ $\frac{3}{4}$ |中，负数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 如图，在△ABC中，AB=AC=4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB，AC于M、N，则△AMN的周长为（）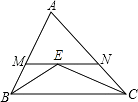

A、12 B、4 C、8 D、不确定

查看试题解析
5. 下列计算正确的是（　　）

A、a+a²=a³ B、a⁶b÷a²=a³b C、（a﹣b）²=a²﹣b² D、（﹣ab³）²=a²b⁶

查看试题解析
6. 在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是 $\frac{2}{5}$ ，如再往盒中放进3颗黑色棋子，取得白色棋子的概率变为 $\frac{1}{4}$ ，则原来盒里有白色棋子（　　）

A、1颗 B、2颗 C、3颗 D、4颗

查看试题解析
7. 下列几何体中，正视图、左视图、俯视图完全相同的是（）

A、圆柱 B、圆锥 C、棱锥 D、球

查看试题解析
8. 如图，⊙O是△ABC的外接圆，弦AC的长为3，sinB= $\frac{3}{4}$ ，则⊙O的半径为（）

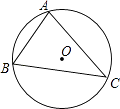A、4 B、3 C、2 D、 $\sqrt{3}$

查看试题解析
9. 如图，点A、B、C、在一次函数y=﹣2x+m的图象上，它们的横坐标依次为﹣1、1、2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（）

A、1 B、3 C、3（m﹣1） D、1.5m﹣3

查看试题解析
10. 已知二次函数y=ax²﹣bx+0.5b﹣a与x轴交于A、B两点，则线段AB的最小值为（）

A、0.5 B、2 C、 $\sqrt{3}$ D、无法确定

查看试题解析

二、填空题：

11. 若ab=3，a﹣2b=5，则a²b﹣2ab²的值是．

查看试题解析
12. 已知x₁、x₂是方程x²﹣4x﹣12=0的解，则x₁+x₂= ．

查看试题解析
13. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为．

查看试题解析
14. 甲、乙玩猜数字游戏，游戏规则如下：有四个数字0、1、2、3，先由甲心中任选一个数字，记为m，再由乙猜甲刚才所选的数字，记为n．若m、n满足|m﹣n|≤1，则称甲、乙两人“心有灵犀”，则甲、乙两人“心有灵犀”的概率是．

查看试题解析
15. 如图，AB为半圆O的直径，C、D是半圆上的三等分点，若⊙O的半径为1，E为线段AB上任意一点，则图中阴影部分的面积为．

查看试题解析
16.
如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP= ．

查看试题解析

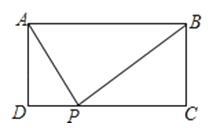
三、计算题：

17. 计算：（﹣1）²⁰¹⁶+2sin60°﹣|﹣ $\sqrt{3}$ |+π⁰ ．

查看试题解析
18. 先化简，再求值： $\frac{a^{2} - b^{2}}{a^{2} - 2 a b + b^{2}}$ • $\frac{a - b}{a + b}$ ﹣ $\frac{a}{a - b}$ ，其中a=1+ $\sqrt{3}$ ，b=1﹣ $\sqrt{3}$ ．

查看试题解析

四、解答题：

19. 如图1，在△ABC中，点D在边BC上，∠ABC：∠ACB：∠ADB=1：2：3，⊙O是△ABD的外接圆．

(1)、求证：AC是⊙O的切线；

(2)、当BD是⊙O的直径时（如图2），求∠CAD的度数．

查看试题解析
20. 每年11月的最后一个星期四是感恩节，小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人．他将调查结果分为如下四类：A类﹣﹣当面致谢；B类﹣﹣打电话；C类﹣﹣发短信息或微信；D类﹣﹣写书信．他将调查结果绘制成如图不完整的扇形统计图和条形统计图：
请你根据图中提供的信息完成下列各题：

(1)、补全条形统计图；

(2)、在A类的同学中，有3人来自同一班级，其中有1人学过主持．现准备从他们3人中随机抽出两位同学主持感恩节主题班会课，请你用树状图或表格求出抽出的两人都没有学过主持的概率．

查看试题解析
21. 如图，为了测量某建筑物BC的高度，小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地而上向建筑物前进了50m到达D处，此时遇到一斜坡，坡度i=1： $\sqrt{3}$ ，沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°，（坡度i=1： $\sqrt{3}$ 是指坡面的铅直高度FE与水平宽度DE的比）．请你计算出该建筑物BC的高度．（取 $\sqrt{3}$ =1.732，结果精确到0.1m）．

查看试题解析
22. 南博汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为29万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出4辆．如果设每辆汽车降价x万元，每辆汽车的销售利润为y万元．（销售利润=销售价﹣进货价）

(1)、求y与x的函数关系式；在保证商家不亏本的前提下，写出x的取值范围；

(2)、假设这种汽车平均每周的销售利润为z万元，试写出z与x之间的函数关系式；

(3)、当每辆汽车的定价为多少万元时，平均每周的销售利润最大，最大利润是多少？

查看试题解析

五、综合题：

23. 在数学兴趣小组活动中，小明进行数学探究活动，将边长为 $\sqrt{2}$ 的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线l上，AB与AG在同一直线上．

(1)、图1中，小明发现DG=BE，请你帮他说明理由．

(2)、小明将正方形ABCD按如图2那样绕点A旋转一周，旋转到当点C恰好落在直线l上时，请你直接写出此时BE的长．

查看试题解析
24. 在平面直角坐标系xOy中，抛物线y=x²+bx+c与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3，0），将直线y=kx沿y轴向上平移3个单位长度后恰好经过B，C两点．

(1)、求直线BC及抛物线的解析式；

(2)、设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求点P的坐标；

(3)、连接CD，求∠OCA与∠OCD两角和的度数．

查看试题解析