初中数学华师大版八年级下学期 第17章测试卷
试卷更新日期:2021-03-19 类型:单元试卷
一、单选题
-
1. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、 为任意实数2. 在函数 中,自变量x的取值范围是( )A、x>2 B、x≤2且x≠0 C、x<2 D、x>2且x≠03. 已知第二象限的点P(﹣4,1),那么点P到x轴的距离为( )A、1 B、4 C、﹣3 D、34. 某游泳池水深 ,现需换水,每小时水位下降 ,那么剩下的高度 与时间 (小时)的关系图象表示为( )A、
 B、
B、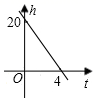 C、
C、 D、
D、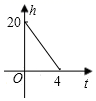 5. 在平面直角坐标系中,点M,N,P,Q的位置如图所示.若直线y = kx经过第一、三象限,则直线y = kx - 2可能经过的点是( )
5. 在平面直角坐标系中,点M,N,P,Q的位置如图所示.若直线y = kx经过第一、三象限,则直线y = kx - 2可能经过的点是( ) A、点M B、点N C、点P D、点Q6. 经过原点的直线 与反比例函数 的图象交于点 A(-3,a) , B(b,-2) ,则k的值为( )A、-2 B、-3 C、-5 D、-67. 对于反比例函数y= ,下列判断正确的是( )A、图象经过点(-1,3) B、图象在第二、四象限 C、不论x为何值,y>0 D、图象所在的第一象限内,y随x的增大而减小8. 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度ρ也随之改变.p与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( )
A、点M B、点N C、点P D、点Q6. 经过原点的直线 与反比例函数 的图象交于点 A(-3,a) , B(b,-2) ,则k的值为( )A、-2 B、-3 C、-5 D、-67. 对于反比例函数y= ,下列判断正确的是( )A、图象经过点(-1,3) B、图象在第二、四象限 C、不论x为何值,y>0 D、图象所在的第一象限内,y随x的增大而减小8. 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度ρ也随之改变.p与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( )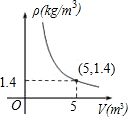 A、1.4kg B、5kg C、6.4kg D、7kg
A、1.4kg B、5kg C、6.4kg D、7kg二、填空题
-
9. 在函数 中,自变量x的取值范围是 .10. 如图所示,在平面直角坐标系中,点P(x,y)是直线y = - x + 6上第一象限的点,点A的坐标是(4,0),O是坐标原点,△PAO的面积为S,则S关于x的函数表达式为 .
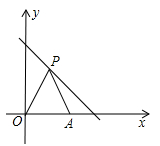 11. 为了迎接学校“歌咏比赛”的到来,九年级学生组织了一个梯形鲜花队参加开幕式,要求共站20排,第一排10人,以后每一排都比前一排多站一人,则某排人数y与该排排数x之间的函数关系式为.(写出自变量的取值范围).12. 如图,已知点C为反比例函数 上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC的面积为.
11. 为了迎接学校“歌咏比赛”的到来,九年级学生组织了一个梯形鲜花队参加开幕式,要求共站20排,第一排10人,以后每一排都比前一排多站一人,则某排人数y与该排排数x之间的函数关系式为.(写出自变量的取值范围).12. 如图,已知点C为反比例函数 上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC的面积为.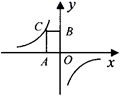
三、综合题
-
13. 已知 与x成正比例,且 时, .(1)、求y与x之间的函数关系式;(2)、当 时,求x的值;(3)、若点 在这个函数图象上,求a的值;(4)、试判断 是否在这个一次函数的图象上;(5)、将该函数图象向左平移2个单位后的函数表达式是什么?14. 在弹性限度内,弹簧的长度y(cm)是所挂物体质量X(kg)的一次函数.某弹簧不挂物体时,长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm.(1)、写出y与x之间的关系式;(2)、并求当所挂物体的质量为4kg时弹簧的长度.15. 为了美化校园,某学校决定利用现有的332盆甲种花卉和310盆乙种花卉,搭配A,B两种园艺造型共50个,摆放在校园道路两侧.已知一个A种园艺造型需甲种花卉7盆,乙种花卉5盆;一个B种园艺造型需甲种花卉6盆,乙种花卉8盆.(1)、问搭配A,B两种园艺造型共有几种方案?(2)、若一个A种园艺造型的成本是200元,一个B种园艺造型的成本是300元,哪种方案成本最低?请写出此方案.16. 如图,平行于y轴的直尺(一部分)与双曲线y= (x>0)交于点A和C,与x轴交于点B和D,点A和B的刻度分别为5cm和2cm,直尺的宽度为2cm,OB=2cm.(注:平面直角坐标系内一个单位长度为1cm)
 (1)、点A的坐标为;(2)、求双曲线y= 的解析式;(3)、若经过A,C两点的直线解析式为y=mx+b,请直接写出关于x的不等式mx+b- <0的解集.
(1)、点A的坐标为;(2)、求双曲线y= 的解析式;(3)、若经过A,C两点的直线解析式为y=mx+b,请直接写出关于x的不等式mx+b- <0的解集.