广东省中山市小榄镇2016-2017学年中考数学一模试卷
试卷更新日期:2017-10-26 类型:中考模拟
一、选择题
-
1. 2017的倒数是( )A、﹣2017 B、2017 C、﹣ D、2. 下列计算正确的是( )A、 × = B、x8÷x2=x4 C、(2a)3=6a3 D、3a3•2a2=6a63. 分解因式:x2y﹣4y结果正确的是( )A、y(x2﹣4) B、y(x﹣2)2 C、y(x+2)2 D、y(x+2)(x﹣2)4. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
 A、70° B、100° C、110° D、80°5. 下列图形中,不是轴对称图形的是( )A、
A、70° B、100° C、110° D、80°5. 下列图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 计算3 ﹣4 的结果是( )A、 B、﹣ C、7 D、﹣17. 一元二次方程x2﹣4x+4=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定8. 函数y= 中,自变量x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤19. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
6. 计算3 ﹣4 的结果是( )A、 B、﹣ C、7 D、﹣17. 一元二次方程x2﹣4x+4=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定8. 函数y= 中,自变量x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤19. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A、1:2 B、1:3 C、1:4 D、1:1610. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )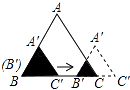 A、
A、 B、
B、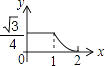 C、
C、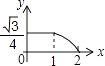 D、
D、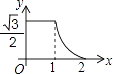
二、填空题
-
11. 已知∠A=80°,那么∠A补角为度.12. 据报道,2016年单位就业人员年平均工资超过70300元,将数70300用科学记数法表示为 .13. 反比例函数y= 的图象经过点(2,3),则k= .14. 如图,EF为△ABC的中位线,△AEF的面积为6,则四边形EBCF的面积为 .
 15. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .
15. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .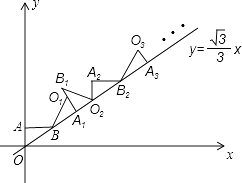
三、解答题(一)
-
16. 计算:( )﹣2﹣6sin30°﹣(π+2017)0+ .17. 解方程: = .18. 先化简,再求值:(2a+b)2﹣a(4a+3b),其中a=1,b= .
四、解答题(二)
-
19. 如图,点O是线段AB和线段CD的中点.
 (1)、求证:△AOD≌△BOC;(2)、求证:AD∥BC.20. 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
(1)、求证:△AOD≌△BOC;(2)、求证:AD∥BC.20. 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50° (1)、求B,C的距离.(2)、通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)21. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
(1)、求B,C的距离.(2)、通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)21. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.五、解答题
-
22. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
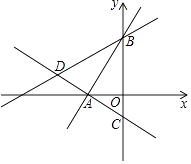 (1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求点D的坐标.23. 如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求点D的坐标.23. 如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点. (1)、求证:△PCE≌△EDQ;(2)、延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(1)、求证:△PCE≌△EDQ;(2)、延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形; (3)、如图3,若△ARB∽△PEQ,求∠MON大小
(3)、如图3,若△ARB∽△PEQ,求∠MON大小 24. 如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
24. 如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.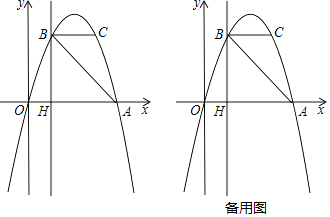 (1)、求抛物线的表达式;(2)、点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(3)、若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
(1)、求抛物线的表达式;(2)、点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(3)、若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.