甘肃省张掖市临泽二中2016-2017学年中考数学三模试卷

试卷更新日期：2017-10-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 9的平方根是（）

A、±3 B、 $\pm \sqrt{3}$ C、3 D、 $\sqrt{3}$

查看试题解析
2. 如图是某工厂要设计生产的正六棱柱形密封罐的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 据统计2014年我国高新技术产品出口总额40570亿元，将数据40570亿用科学记数法表示为（）

A、4.0570×10⁹ B、0.40570×10¹⁰ C、40.570×10¹¹ D、4.0570×10¹²

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、（m²）³=m⁵ C、a²•a³=a⁵ D、（x+y）²=x²+y²

查看试题解析
5. 下列命题中的假命题是（）

A、一组邻边相等的平行四边形是菱形 B、一组邻边相等的矩形是正方形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等且有一个角是直角的四边形是矩形

查看试题解析
6. 不等式组 ${\begin{matrix} 3 x + 2 > 5 \\ 5 - 2 x \geq 1 \end{matrix}$ 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
7.
如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

A、40° B、35° C、30° D、45°

查看试题解析
8. 已知点A，B分别在反比例函数y= $\frac{2}{x}$ （x＞0），y= $\frac{- 8}{x}$ （x＞0）的图象上且OA⊥OB，则tanB为（）

A、 $\frac{1}{\sqrt{2}}$ B、 $\frac{1}{2}$ C、 $\frac{1}{\sqrt{3}}$ D、 $\frac{1}{3}$

查看试题解析
9. 抛物线y=ax²+bx+c（a≠0）的图象如图所示，则下列说法正确的是（）

A、b²﹣4ac＜0 B、abc＜0 C、 $- \frac{b}{2 a} < - 1$ D、a﹣b+c＜0

查看试题解析

二、填空题

10. 分解因式：x³﹣4x= ．

查看试题解析
11. 函数y= $\sqrt{2 - x} + \frac{1}{x - 1}$ 中自变量x的取值范围是．

查看试题解析
12. 分式方程 $\frac{2}{x} = \frac{5}{x + 3}$ 的解是．

查看试题解析
13. 如图，在△ABC中，∠C=120°，AB=4cm，两等圆⊙A与⊙B外切，则图中两个扇形（即阴影部分）的面之和为cm² ．（结果保留π）．

查看试题解析
14. 计算： $(a + \frac{2 a b}{a - b}) \div \frac{a + b}{a - b}$ = ．

查看试题解析
15. 如图，在⊙O中，弦AB，CD相交于点P．若∠A=40°，∠APD=75°，则∠B= ．

查看试题解析
16. 在临桂新区建设中，需要修一段全长2400m的道路，为了尽量减少施工对县城交通工具所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度．若设原计划每天修路xm，则根据题意可得方程．

查看试题解析
17. 如图，已知等腰Rt△ABC的直角边为1，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边．画第三个Rt△ADE，…，依此类推直到第五个等腰Rt△AFG，则由这五个等腰直角三角形所构成的图形的面积为．

查看试题解析

三、解答题

18. 计算：| $\sqrt{3}$ ﹣2|﹣（π﹣2015）⁰+（﹣ $\frac{1}{2}$ ）^﹣²﹣2sin60°+ $\sqrt{12}$ ．

查看试题解析
19. 已知x=1是关于x的一元二次方程x²﹣4mx+m²=0的根，求代数式 $2 m (m - 2) - (m + \sqrt{3}) (m - \sqrt{3})$ 的值．

查看试题解析
20. 如图所示，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A，B的坐标分别是A（3，3）、B（1，2），△AOB绕点O逆时针旋转90°后得到△A₁OB₁ ．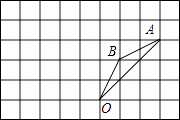

(1)、画出△A₁OB₁ ，直接写出点A₁ ， B₁的坐标；

(2)、在旋转过程中，点B经过的路径的长．

查看试题解析
21. 有三张卡片（形状、大小、颜色、质地都相等），正面分别写上整式x²+1，﹣x²﹣2，3．将这三张卡片背面向上洗匀，从中任意抽取一张卡片，记卡片上的整式为A，再从剩下的卡片中任意抽取一张，记卡片上的整式为B，于是得到代数式 $\frac{A}{B}$ ．

(1)、请用画树状图或列表的方法，写出代数式 $\frac{A}{B}$ 所有可能的结果；

(2)、求代数式 $\frac{A}{B}$ 恰好是分式的概率．

查看试题解析
22. 某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度，抽取部分学生进行调查．被调查的每个学生按A（非常喜欢）、B（比较喜欢）、C（一般）、D（不喜欢）四个等级对活动评价．图（1）和图（2）是该小组采集数据后绘制的两幅统计图．经确认扇形统计图是正确的，而条形统计图尚有一处错误且并不完整．请你根据统计图提供的信息，解答下列问题：

(1)、此次调查的学生人数为；

(2)、条形统计图中存在错误的是（填A，B，C中的一个），并在图中加以改正；

(3)、在图（2）中补画条形统计图中不完整的部分；

(4)、如果该校有600名学生，那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人？

查看试题解析
23. 如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠FAE=30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11， $\sqrt{3}$ ≈1.73）

查看试题解析
24. 如图，在平面直角坐标系中，一次函数y=kx+b的图象分别交x轴、y轴于A，B两点，与反比例函数 $y = \frac{m}{x}$ 的图象交于C，D两点，DE⊥x轴于点E，已知C点的坐标是（6，﹣1），DE=3．

(1)、求反比例函数与一次函数的解析式；

(2)、求△CDE的面积．

查看试题解析
25. D，E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB，AC的中点．O是△ABC所在平面上的动点，连接OB，OC，点G，F分别是OB，OC的中点，顺次连接点D，G，F，E．

(1)、如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；

(2)、若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）

查看试题解析
26. 如图，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．

(1)、求证：BC是⊙O的切线；

(2)、连接AF、BF，求∠ABF的度数；

(3)、如果BE=10，sinA= $\frac{5}{13}$ ，求⊙O的半径．

查看试题解析
27. 如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax²+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

(1)、直接写出点A的坐标，并求出抛物线的解析式；

(2)、过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？

(3)、在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

查看试题解析