甘肃省兰州三十一中2016-2017学年中考数学模拟试卷

试卷更新日期：2017-10-26 类型：中考模拟

进入出卷网下载

一、选择题：

1. 与如图所示的三视图对应的几何体是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程x²+4x﹣3=0的两根为x₁、x₂ ，则x₁•x₂的值是（）

A、4 B、﹣4 C、3 D、﹣3

查看试题解析
3. 在平面直角坐标系中，抛物线y=x²﹣1与x轴交点的个数（）

A、3 B、2 C、1 D、0

查看试题解析
4. 下列说法中正确的是（　　）

A、四边相等的四边形是菱形 B、一组对边相等，另一组对边平行的四边形是菱形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是菱形

查看试题解析
5. 如图，已知在△ABC中，点D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于（）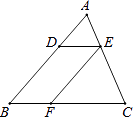

A、5：8 B、3：8 C、3：5 D、2：5

查看试题解析
6. 如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，∠AED=115°，则∠B的度数是（）

A、50° B、75° C、80° D、100°

查看试题解析
7. 反比例函数y=﹣ $\frac{3}{2 x}$ 中常数k为（）

A、﹣3 B、2 C、﹣ $\frac{1}{2}$ D、﹣ $\frac{3}{2}$

查看试题解析
8. 如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（）

A、x＜﹣1 B、x＞2 C、﹣1＜x＜0，或x＞2 D、x＜﹣1，或0＜x＜2

查看试题解析
9. 某厂改进工艺降低了某种产品的成本，两个月内从每件产品250元，降低到了每件160元，平均每月降低率为（　　）

A、15% B、20% C、5% D、25%

查看试题解析
10. 如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB= $\frac{1}{2}$ BC，连接OE．下列结论：①∠CAD=30°；②S_▱ABCD=AB•AC；③OB=AB；④OE= $\frac{1}{4}$ BC，成立的个数有（）

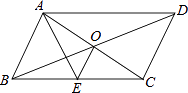A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 圆的半径扩大一倍，则它的相应的圆内接正n边形的边长与半径之比（）

A、扩大了一倍 B、扩大了两倍 C、扩大了四倍 D、没有变化

查看试题解析
12. 心理学家发现：学生对概念的接受能力y与提出概念的时间x（min）之间是二次函数关系，当提出概念13min时，学生对概念的接受力最大，为59.9；当提出概念30min时，学生对概念的接受能力就剩下31，则y与x满足的二次函数关系式为（）

A、y=﹣（x﹣13）²+59.9 B、y=﹣0.1x²+2.6x+31 C、y=0.1x²﹣2.6x+76.8 D、y=﹣0.1x²+2.6x+43

查看试题解析
13. 在△ABC中，若cosA= $\frac{\sqrt{2}}{2}$ ，tanB= $\sqrt{3}$ ，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
14. 如图，正方形OABC的边长为2，OA与x轴负半轴的夹角为15°，点B在抛物线y=ax²（a＜0）的图象上，则a的值为（）

A、 $- \frac{1}{2}$ B、 $- \frac{\sqrt{2}}{6}$ C、﹣2 D、 $- \frac{\sqrt{2}}{3}$

查看试题解析

二、填空题

15. 把一元二次方程（x+1）（1﹣x）=2x化成二次项系数大于零的一般式是，其中二次项系数是，一次项的系数是，常数项是；

查看试题解析
16. 如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH是矩形．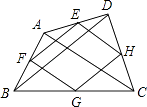

查看试题解析
17. 如图，在▱ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF=.

查看试题解析
18. 一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD是水平的，BC与水平面的夹角为60°，其中AB=60cm，CD=40cm，BC=40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为cm．

查看试题解析
19. 如图，在正方形ABCD中，点E是BC边上一点，且BE：EC=2：1，AE与BD交于点F，则△AFD与四边形DFEC的面积之比是．

查看试题解析

三、计算题

20. 计算：（π﹣3.14）⁰+| $\sqrt{2}$ ﹣1|﹣（ $\frac{\sqrt{2}}{2}$ ）^﹣¹﹣2sin45°+（﹣1）²⁰¹⁶ ．

查看试题解析
21. 配方法解：x²+3x﹣4=0．

查看试题解析

四、解答题

22. 图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．

(1)、在图1中画出钝角△ABC，使它的面积为6（画一个即可）；

(2)、在图2中画出△DEF，使它的三边长分别为 $\sqrt{5}$ 、2 $\sqrt{5}$ 、5（画一个即可）．并且直接写出此时三角形DEF的面积．

查看试题解析
23. 八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：
类别
频数（人数）
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
m
1

(1)、计算m=；

(2)、在扇形统计图中，“其他”类所占的百分比为；

(3)、在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．

查看试题解析
24. 为方便市民通行，某广场计划对坡角为30°，坡长为60米的斜坡AB进行改造，在斜坡中点D处挖去部分坡体（阴影表示），修建一个平行于水平线CA的平台DE和一条新的斜坡BE．

(1)、若修建的斜坡BE的坡角为36°，则平台DE的长约为多少米？

(2)、在距离坡角A点27米远的G处是商场主楼，小明在D点测得主楼顶部H 的仰角为30°，那么主楼GH高约为多少米？（结果取整数，参考数据：sin36°=0.6，cos36°=0.8，tan36°=0.7， $\sqrt{3}$ =1.7）

查看试题解析
25. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE= $\frac{1}{2}$ AC，连接AE交OD于点F，连接CE、OE．

(1)、求证：OE=CD；

(2)、若菱形ABCD的边长为4，∠ABC=60°，求AE的长．

查看试题解析
26. 一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，前2分钟其速度v（米/分）与时间t（分）满足二次函数v=at² ，后三分钟其速度v（米/分）与时间t（分）满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分，求：

(1)、二次函数和反比例函数的关系式．

(2)、弹珠在轨道上行驶的最大速度．

(3)、求弹珠离开轨道时的速度．

查看试题解析
27. 如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，在AC延长线上有一点E，满足AD²=AB•AE．
求证：DE是⊙O的切线．

查看试题解析
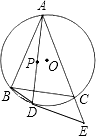28. 如图，在平面直角坐标系中，直线AB交x轴于点A（5，0），交y轴于点B，AO是⊙M的直径，其半圆交AB于点C，且AC=3．取BO的中点D，连接CD、MD和OC．

(1)、求证：CD是⊙M的切线；

(2)、二次函数的图象经过点D、M、A，其对称轴上有一动点P，连接PD、PM，求△PDM的周长最小时点P的坐标；

(3)、在（2）的条件下，当△PDM的周长最小时，抛物线上是否存在点Q，使S_△_QAM= $\frac{1}{6}$ S_△_PDM？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

类别	频数（人数）	频率
小说		0.5
戏剧	4
散文	10	0.25
其他	6
合计	m	1