2016年湖北省孝感市中考数学试卷
试卷更新日期:2016-07-21 类型:中考真卷
一、选择题
-
1. 下列各数中,最小的数是( )
A、5 B、﹣3 C、0 D、22.如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2等于( )
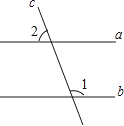 A、70° B、75° C、80° D、85°3. 下列运算正确的是( )A、a2+a2=a4 B、a5﹣a3=a2 C、a2•a2=2a2 D、(a5)2=a104.
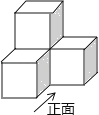
A、70° B、75° C、80° D、85°3. 下列运算正确的是( )A、a2+a2=a4 B、a5﹣a3=a2 C、a2•a2=2a2 D、(a5)2=a104.如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集是( )
5. 不等式组 的解集是( )
A、x>3 B、x<3 C、x<2 D、x>26.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
 A、( ,﹣1) B、(1,﹣ ) C、( ,﹣ ) D、(﹣ , )7. 在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )
A、( ,﹣1) B、(1,﹣ ) C、( ,﹣ ) D、(﹣ , )7. 在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )成绩(分)
27
28
30
人数
2
3
1
A、28,28,1 B、28,27.5,1 C、3,2.5,5 D、3,2,58. “科学用眼,保护视力”是青少年珍爱生命的具体表现.科学证实:近视眼镜的度数y(度)与镜片焦距x(m)成反比例.如果500度近视眼镜片的焦距为0.2m,则表示y与x函数关系的图象大致是( )A、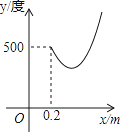 B、
B、 C、
C、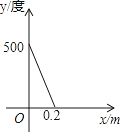 D、
D、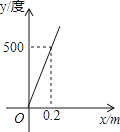 9. 在▱ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )A、3 B、5 C、2或3 D、3或510.
9. 在▱ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )A、3 B、5 C、2或3 D、3或510.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
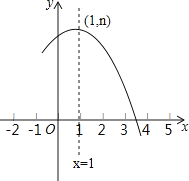 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若代数式 有意义,则x的取值范围是 .
12. 分解因式:2x2﹣8y2= .
13. 若一个圆锥的底面圆半径为3cm,其侧面展开图的圆心角为120°,则圆锥的母线长是cm.
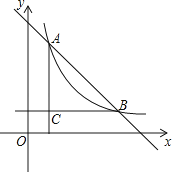
14. 《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是步.15.如图,已知双曲线y= 与直线y=﹣x+6相交于A,B两点,过点A作x轴的垂线与过点B作y轴的垂线相交于点C,若△ABC的面积为8,则k的值为
 16.
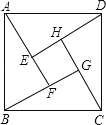
16.如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为
三、解答题
-
17. 计算: +|﹣4|+2sin30°﹣32 .18.
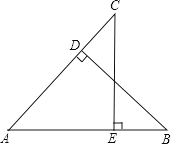
如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
 19.
19.为弘扬中华优秀传统文化,我市教育局在全市中小学积极推广“太极拳”运动.弘孝中学为争创“太极拳”示范学校,今年3月份举行了“太极拳”比赛,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
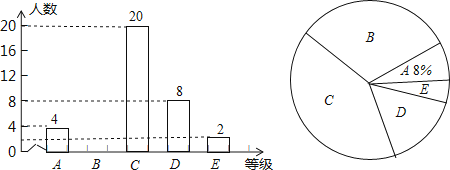 (1)、该校七(1)班共有△名学生;扇形统计图中C等级所对应扇形的圆心角等于△度;并补全条形统计图;
(1)、该校七(1)班共有△名学生;扇形统计图中C等级所对应扇形的圆心角等于△度;并补全条形统计图;
(2)、A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生作为全班训练的示范者,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
20.如图,在Rt△ABC中,∠ACB=90°.
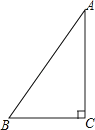 (1)、请用直尺和圆规按下列步骤作图,保留作图痕迹:
(1)、请用直尺和圆规按下列步骤作图,保留作图痕迹:①作∠ACB的平分线,交斜边AB于点D;
②过点D作AC的垂线,垂足为点E.
(2)、在(1)作出的图形中,若CB=4,CA=6,则DE=
21. 已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .(1)、求m的取值范围;(2)、当x12+x22=6x1x2时,求m的值.22. 孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.(1)、求A种,B种树木每棵各多少元?(2)、因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.23.如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
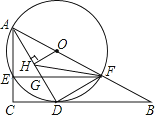 (1)、求证:AD平分∠CAB;(2)、若OH⊥AD于点H,FH平分∠AFE,DG=1.
(1)、求证:AD平分∠CAB;(2)、若OH⊥AD于点H,FH平分∠AFE,DG=1.①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
24.在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
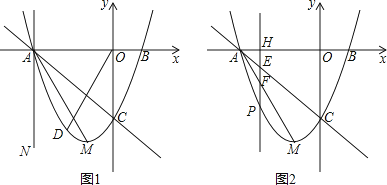 (1)、填空:b= , c= , 直线AC的解析式为
(1)、填空:b= , c= , 直线AC的解析式为
(2)、直线x=t与x轴相交于点H.①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为 ,求此时t的值.