安徽省芜湖二十九中2016-2017学年中考数学一模试卷

试卷更新日期：2017-10-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的有（）

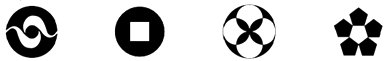A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 如图，点D，E分别为△ABC的边AB，AC上的中点，则△ADE的面积与四边形BCED的面积的比为（）

A、1：2 B、1：3 C、1：4 D、1：1

查看试题解析
3. 如图，点A的坐标是（2，0），△ABO是等边三角形，点B在第一象限．若反比例函数y= $\frac{k}{x}$ 的图象经过点B，则k的值是（）

A、1 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
4. 如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）

A、 $\frac{A B}{B P}$ = $\frac{A C}{C B}$ B、∠APB=∠ABC C、 $\frac{A P}{A B}$ = $\frac{A B}{A C}$ D、∠ABP=∠C

查看试题解析
5. 在△ABC中，（2cosA﹣ $\sqrt{2}$ ）²+|1﹣tanB|=0，则△ABC一定是（　　）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
6. 已知x=1是方程x²+bx=2的一个根，则方程的另一个根是（）

A、1 B、2 C、﹣2 D、﹣1

查看试题解析
7. 有四张背面一模一样的卡片，卡片正面分别写着一个函数关系式，分别是y=2x，y=x²﹣3（x＞0），y= $\frac{2}{x}$ （x＞0），y=﹣ $\frac{1}{3 x}$ （x＜0），将卡片顺序打乱后，随意从中抽取一张，取出的卡片上的函数是y随x的增大而增大的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
8. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（）

A、a＞0 B、3是方程ax²+bx+c=0的一个根 C、a+b+c=0 D、当x＜1时，y随x的增大而减小

查看试题解析
9. 如图所示，直线l和反比例函数y= $\frac{k}{x}$ （k＞0）的图象的一支交于A，B两点，P是线段AB上的点（不与A，B重合），过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接OA，OB，OP，设△AOC面积是S₁ ， △BOD面积是S₂ ， △POE面积是S₃ ，则（）

A、S₁＜S₂＜S₃ B、S₁＞S₂＞S₃ C、S₁=S₂＞S₃ D、S₁=S₂＜S₃

查看试题解析
10. 如图，⊙O是△ABC的外接圆，弦AC的长为3，sinB= $\frac{3}{4}$ ，则⊙O的半径为（）

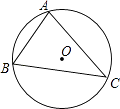A、4 B、3 C、2 D、 $\sqrt{3}$

查看试题解析

二、填空题

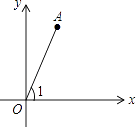
11. 如图，若点A的坐标为 $(1 ， \sqrt{3})$ ，则sin∠1= ．

查看试题解析
12. 如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若OD=2，tan∠OAB= $\frac{1}{2}$ ，则AB的长是．

查看试题解析
13. 如图，一次函数与反比例的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是．

查看试题解析
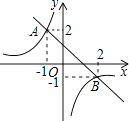14. 在矩形ABCD中，AB=6，BC=8，AC，BD相交于O，P是边BC上一点，AP与BD交于点M，DP与AC交于点N．
①若点P为BC的中点，则AM：PM=2：1；
②若点P为BC的中点，则四边形OMPN的面积是8；
③若点P为BC的中点，则图中阴影部分的总面积为28；
④若点P在BC的运动，则图中阴影部分的总面积不变．
其中正确的是．（填序号即可）

查看试题解析

三、解答题

15. 计算：（ $\sqrt{2}$ ﹣1）⁰+（﹣1）²⁰¹⁵+（ $\frac{1}{3}$ ）^﹣¹﹣2sin30°．

查看试题解析
16. 解方程：x²﹣5x+3=0．

查看试题解析

四、综合题

17. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点四边形ABCD（顶点是网格线的交点），按要求画出四边形AB₁C₁D₁和四边形AB₂C₂D₂ ．

(1)、以A为旋转中心，将四边形ABCD顺时针旋转90°，得到四边形AB₁C₁D₁；

(2)、以A为位似中心，将四边形ABCD作位似变换，且放大到原来的两倍，得到四边形AB₂C₂D₂ ．

查看试题解析
18.
如图，专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处，同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上．已知B在A的正东方向，且相距100里，请分别求出两艘船到达事发地点C的距离．（注：里是海程单位，相当于一海里．结果保留根号）

查看试题解析

五、应用题

19. 如图，在平面直角坐标系xOy中，直线y=﹣ $\frac{1}{2}$ x+2分别与x、y轴交于点B、A，与反比例函数的图象分别交于点C、D，CE⊥x轴于点E，OE=2．

(1)、求反比例函数的解析式；

(2)、连接OD，求△OBD的面积．

(3)、x取何值时，反比例函数的值大于一次函数的值.

查看试题解析
20. 如图，已知△ABC为直角三角形，∠C=90°，边BC是⊙0的切线，切点为D，AB经过圆心O并与圆相交于点E，连接AD．

(1)、求证：AD平分∠BAC；

(2)、若AC=8，tan∠DAC= $\frac{3}{4}$ ，求⊙O的半径．

查看试题解析
21. 在一个不透明的袋子中装有仅颜色不同的5个小球，其中红球3个，黑球2个．

(1)、先从袋中取出m（m＞1）个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A，填空：若A为必然事件，则m的值为，若A为随机事件，则m的取值为；

(2)、若从袋中随机摸出2个球，正好红球、黑球各1个，求这个事件的概率．

查看试题解析
22. 如图1，在四边形ABCD中，∠DAB被对角线AC平分，且AC²=AB•AD，我们称该四边形为“可分四边形”，∠DAB称为“可分角”．

(1)、如图2，若四边形ABCD为“可分四边形”，∠DAB为“可分角”，且∠DCB=∠DAB，则∠DAB=°．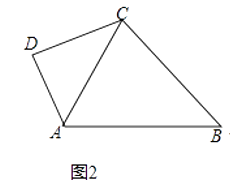

(2)、如图3，在四边形ABCD中，∠DAB=60°，AC平分∠DAB，且∠BCD=150°，求证：四边形ABCD为“可分四边形”；

(3)、现有四边形ABCD为“可分四边形”，∠DAB为“可分角”，且AC=4，BC=2，∠D=90°，求AD的长？

查看试题解析
23. 已知抛物线l₁：y=﹣x²+2x+3与x轴交于点A、B（点A在点B左边），与y轴交于点C，抛物线l₂经过点A，与x轴的另一个交点为E（4，0），与y轴交于点D（0，﹣2）．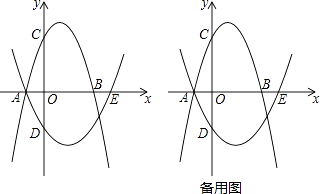

(1)、求抛物线l₂的解析式；

(2)、点P为线段AB上一动点（不与A、B重合），过点P作y轴的平行线交抛物线l₁于点M，交抛物线l₂于点N．
①当四边形AMBN的面积最大时，求点P的坐标；
②当CM=DN≠0时，求点P的坐标．

查看试题解析