安徽省芜湖二十九中2016-2017学年中考数学二模试卷
试卷更新日期:2017-10-26 类型:中考模拟
一、选择题
-
1. ﹣3的倒数是( )A、3 B、﹣3 C、﹣ D、2. 南海资源丰富,其面积约为350万平方千米,相当于我国的渤海、黄海和东海总面积的3倍.其中350万用科学记数法表示为( )A、0.35×108 B、3.5×107 C、3.5×106 D、35×1053. 下列运算正确的是( )A、x4+x2=x6 B、(﹣2a)3•a=6a4 C、(﹣x)6÷x2=x3 D、a2b•(﹣2a2b)=﹣2a4b24. 为调查某班学生每天使用零花钱的情况,张华随机调查了20名同学,结果如下表:
每天使用零花钱(单位:元)
1
2
3
4
5
人数
1
3
6
5
5
则这20名同学每天使用的零花钱的众数和中位数分别是( )
A、3,3 B、3,3.5 C、3.5,3.5 D、3.5,35. 下列四个几何体中,主视图与其它三个不同的是( )A、 B、
B、 C、
C、 D、
D、 6. 餐桌桌面是长为160cm,宽为100cm的长方形,妈妈准备设计一块桌布,面积是桌面的2倍,且使四周垂下的边等宽.若设垂下的桌布宽为xcm,则所列方程为( )A、(160+x)(100+x)=160×100×2 B、(160+2x)(100+2x)=160×100×2 C、(160+x)(100+x)=160×100 D、2(160x+100x)=160×1007. 已知 ,且x﹣y<0,则m的取值范围为( )
6. 餐桌桌面是长为160cm,宽为100cm的长方形,妈妈准备设计一块桌布,面积是桌面的2倍,且使四周垂下的边等宽.若设垂下的桌布宽为xcm,则所列方程为( )A、(160+x)(100+x)=160×100×2 B、(160+2x)(100+2x)=160×100×2 C、(160+x)(100+x)=160×100 D、2(160x+100x)=160×1007. 已知 ,且x﹣y<0,则m的取值范围为( )
A、m B、m C、m D、m8. 如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是 上一点,则∠APB的度数为( ) A、30° B、45° C、60° D、75°9. 如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( )
A、30° B、45° C、60° D、75°9. 如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( ) A、1:2 B、1:3 C、1:4 D、2:310. 如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )
A、1:2 B、1:3 C、1:4 D、2:310. 如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )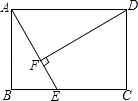 A、
A、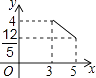 B、
B、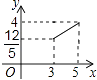 C、
C、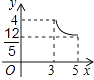 D、
D、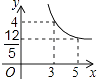
二、填空题
-
11. 分解因式:xy2﹣9x .12. 制作一个圆锥模型,要求圆锥母线长9cm,底面圆直径为10cm,那么要制作的这个圆锥模型的侧面展开扇形的纸片圆心角度数是度.
 13. 在如图所示的数轴上,点C与点B关于点A对称,C、A两点对应的实数分别是 和1,则点B对应的实数为 .
13. 在如图所示的数轴上,点C与点B关于点A对称,C、A两点对应的实数分别是 和1,则点B对应的实数为 . 14. 如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:
14. 如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:①四边形EFGP是菱形;
②△PED为等腰三角形;
③若∠ABD=90°,则△EFP≌△GPD;
④若四边形FPDG也是平行四边形,则BC∥AD且∠CDA=60°.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).

三、综合题
-
15. 计算:﹣2cos30°+()﹣2﹣|1﹣|.16. 先化简再求值: ,其中x是方程x2=2x的根.
四、解答题
-
17. 观察下列算式:
①1×5+4=32 ,
②2×6+4=42 ,
③3×7+4=52 ,
④4×8+4=62 ,
…
请你在察规律解决下列问题
(1)、填空:×+4=20152 .(2)、写出第n个式子(用含n的式子表示),并证明.18. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
①把△ABC绕点O顺时针旋转90°得到△A1B1C1;
②以图中的O为位似中心,在△A1B1C1的同侧将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 .
五、解答题
-
19. 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度( , )
 20. 如图,一次函数y1=kx+b和反比例函数y2= 的图象交于A、B两点.
20. 如图,一次函数y1=kx+b和反比例函数y2= 的图象交于A、B两点. (1)、求一次函数y1=kx+b和反比例函数y2= 的解析式;(2)、观察图象写出y1<y2时,x的取值范围为;(3)、求△OAB的面积.
(1)、求一次函数y1=kx+b和反比例函数y2= 的解析式;(2)、观察图象写出y1<y2时,x的取值范围为;(3)、求△OAB的面积.六、解答题
-
21. 为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
七、解答题
-
22. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
 (1)、求证:AC2=AB•AD;(2)、求证:CE∥AD;(3)、若AD=5,AB=7,求 的值.
(1)、求证:AC2=AB•AD;(2)、求证:CE∥AD;(3)、若AD=5,AB=7,求 的值.八、应用题
-
23. 如图,已知一条直线过点(0,4),且与抛物线y= x2交于A,B两点,其中点A的横坐标是﹣2.
 (1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
(1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
-
-