初中数学苏科版八年级下册 9.4 菱形的判定及性质 同步训练
试卷更新日期：2021-03-18 类型：同步测试
一、单选题
-
1. 下列命题中，真命题是（ ）.A、对角线相等且互相垂直的四边形是菱形 B、有一条对角线平分对角的四边形是菱形 C、菱形是对角线互相垂直平分的四边形 D、菱形的对角线相等2. 菱形的两条对角线的长分别为6和8，则菱形的高为（ ）A、 B、 C、 D、3.
如图，在平行四边形ABCD中，AC平分∠DAB ， AB＝2，则平行四边形ABCD的周长为（ ）.
A、4 B、6 C、8 D、124. 如图，在 ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（ ）
A、梯形 B、矩形 C、菱形 D、正方形5. 如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D，AF平分∠CAB交CD于E，交CB于F，且EG∥AB交CB于G，则CF与GB的大小关系是（ ）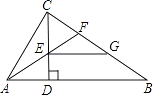
A、CF＞GB B、GB=CF C、CF＜GB D、无法确定6.如图，在菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为（ ）
A、1 B、 C、2 D、7.如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（ ）
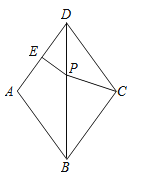A、108° B、72° C、90° D、100°8. 如图，分别以Rt△ABC的斜边AB，直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G．连接EF，若∠BAC＝30°，下列结论：①EF⊥AC；②四边形ADFE为菱形；③AD＝4AG；④△DBF≌△EFA．则正确结论的序号是（ ）
A、①③ B、②④ C、①③④ D、②③④9. 如图，已知线段AB，分别以A，B为圆心，大于 AB同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是（ ）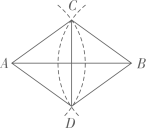
A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD10. 如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上的一点，且CD=DE，连结BE，分别交AC，AD于点F、G，连结OG，则下列结论：①OG= AB；②图中与△EGD全等的三角形共有5个；③由点A、B、D、E构成的四边形是菱形；④S四边形ODGF=S△ABF ， 其中正确的结论是（ ）
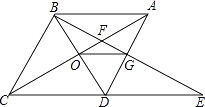A、①③ B、①③④ C、①②③ D、②③④二、填空题
-
11. 菱形两条对角线长分别是4和6，则这个菱形的面积为 ．
12.如图，平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为 ．
13. 如图，在平行四边形ABCD中，∠ABC的平分线BF交AD于点F，FE∥AB．若AB=5，BF=6，则四边形ABEF的面积为 。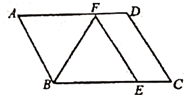
14.如图，在菱形ABCD中，点E是AB上的一点，连接DE交AC于点O，连接BO，且∠AED=50°，则∠CBO= 度．
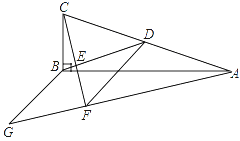
15.如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，CF=6，则四边形BDFG的周长为 ．
16. 在数学课上，老师提出如下问题：尺规作图：过直线外一点作已知直线的平行线．
已知：直线l及其外一点A．
求作：l的平行线，使它经过点A．
小云的作法如下：(1)在直线l上任取一点B；(2)以B为圆心，BA长为半径作弧，交直线l于点C；(3)分别以A、C为圆心，BA长为半径作弧，两弧相交于点D；(4)作直线AD．直线AD即为所求．
小云作图的依据是 ．
三、解答题
-
17.
如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE ， 过点C作CF∥BE交DE的延长线于F ． 求证：四边形BCFE是菱形.
18.在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F
（1）求证：△AEF≌△DEB；
（2）证明：四边形ADCF是菱形；
（3）若AB=4，AC=5，求菱形ADCF的面积．
19.如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°，得到△ADE，连接BD和CE，BD与CE交于点F．
(1)、∠AEC的度数；(2)、求证：四边形ABFE是菱形．20. 如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ.
(1)、求证：四边形BPEQ是菱形；(2)、若AB=6，BE=10，求PQ的长.21. 如图，点E，F分别在正方形ABCD的边DA，DC延长线上，且AE＝CF，连接BE，BF，过点E作EG∥BF，过点F作FG∥BE，EG，FG交于点G.
(1)、求证：四边形BEGF是菱形；(2)、若AD＝3AE＝6，求四边形BEGF的周长.22. 在Rt△ABC中，∠BAC= ，D是BC的中点，E是AD的中点.过点A作AF∥BC交BE的延长线于点F.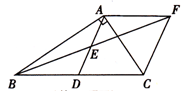
(1)、求证：△AEF≌△DEB；(2)、证明四边形ADCF是菱形；(3)、若AC=4，AB=5，求菱形ADCFD 的面积.23. 如图，在矩形ABCD中，E是AD边上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、QE
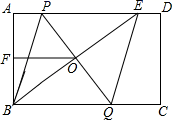(1)、求证：四边形BPEQ是菱形：(2)、若AB＝6，F是AB中点，OF＝4，求菱形BPEQ的面积.24. 如图，在平面直角坐标系中，直线 ∶ 分别与 轴、 轴交于点B、C，且与直线 ∶ 交于点A.
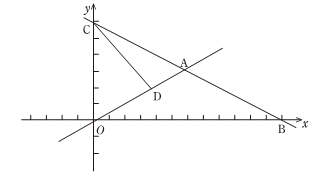(1)、请写出A( ， )，B( ， )，C ( ， ).(2)、若D是线段OA上的一点，且△COD的面积为12，求直线CD的函数表达式.(3)、在(2)的条件下，设P是射线CD上的点，在平面内存在点Q，使以O、C、P、Q为顶点的四边形是菱形，请直接写出Q点的坐标.25. 如图1，有一张矩形纸片ABCD，AB＝4，BC＝8，点M，N分别在矩形的边AD，BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM.
(1)、求证：四边形CMPN是菱形；(2)、当P，A重合时，如图2，求MN的长；(3)、设△PQM的面积为S，求S的取值范围.