初中数学苏科版八年级下册 9.4 菱形的性质 同步训练
试卷更新日期：2021-03-18 类型：同步测试
一、单选题
-
1. 菱形具有而矩形不具有的性质是（ ）A、两组对边分别平行 B、对角线互相垂直 C、对角线互相平分 D、两组对角分别相等2. 如图，菱形ABCD 中，对角线AC，BD相交于点O，下列结论中不一定成立的是（ ）
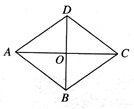A、AB∥DC B、AC=BD C、AC ⊥BD D、OA=OC3. 在平面直角坐标系中，菱形ABCD的顶点的坐标A，B，C分别为（﹣2，0），（0，1），（2，0），则顶点D的坐标为（ ）A、（0，﹣1） B、（﹣2，1） C、（2，1） D、（0，﹣2）4. 已知某菱形的周长为 ，高为 ，则该菱形的面积为（ ）A、 B、 C、 D、5. 如图，菱形ABCD的周长为40cm，对角线AC，BD相交于点O，DE⊥AB，垂足为E，DE：AB=4：5，则下列结论：①DE=8cm；②BE=4cm；③BD=
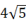cm；④AC= 
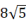cm；⑤S菱形ABCD=80cm，正确的有（ ） 
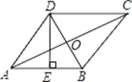A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③⑤6. 在菱形 中 ， ， 边上的高为（ ）A、 B、 C、 D、7. 如图，菱形ABCD边长为5cm，P为对角线BD上一点，PH⊥AB于点H，且PH＝2cm，则△PBC的面积为（ ）cm2 ．
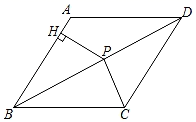A、8 B、7 C、6 D、58. 如图，点P，Q分别是菱形ABCD的边AD，BC上的两个动点，若线段PQ长的最大值为8 ，最小值为8，则菱形ABCD的边长为（ ）
A、4 B、10 C、12 D、169. 如图，菱形ABCD的边长为5，对角线AC的长为8，延长AB至E，BF平分∠CBE，点G是BF上任意一点，则△ACG的面积为（ ）
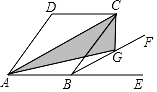A、6 B、12 C、20 D、2410. 在菱形ABCD中，∠ADC=60°，点E为AB边的中点，DE是线段AP的垂直平分线，连接DP、BP、CP，下列结论：①DP=CD；②AP2+BP2=CD2；③∠DCP=75°；④∠CPA=150°，其中正确的是（ ）
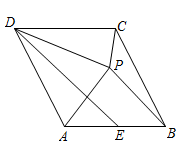A、①② B、①②③ C、①②④ D、①②③④二、填空题
-
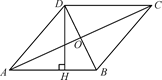
11. 已知菱形ABCD的对角线AC=10，BD=8，则菱形ABCD的面积为.12. 如图，四边形ABCD是菱形，AC＝16，DB＝12，DH⊥AB于点H，则DH等于 ．
13. 如图，在菱形 ABCD 中，E 为 AB 上一点，沿 CE 折叠△BEC，点 B 恰好落在对角线 AC上的 处.若∠DAB=56°，则 的度数为.
14. 如图，菱形纸片ABCD，AB＝4，∠B＝60°，将该菱形纸片折叠，使点B恰好落在CD边的中点B′处，折痕与边BC、BA分别交于点M、N.则BM的长为.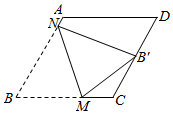
15. 如图，菱形 的边长为2， ，点Q是 的中点，点P是对角线 上一动点，则 最小值为.
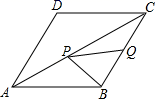16. 如图，在菱形ABCD中，点E是AB上的一点，连结DE交AC于点O，连结BO，且∠AED＝50°，则∠CBO＝度．
17. 蜜蜂采蜜时，如果蜜源很远它就会跳起“8字舞”，告诉同伴蜜源的方向．如图所示，两个全等菱形的边长为1厘米，一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，飞行2020厘米后停下，则这只蜜蜂停在点．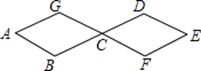
18. 如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为.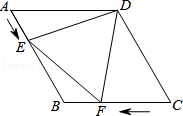
三、解答题
-
19. 如图，在菱形ABCD中，AB=6，∠ABD=30°，求菱形ABCD的面积.
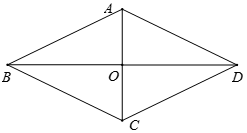20. 如图，已知在菱形ABCD中，∠ABC＝60°，对角线AC＝8，求菱形ABCD的周长和面积．
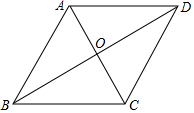21. 已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E．求证：∠AFD＝∠CBE．
22.用一张长12cm宽5cm的矩形纸片折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH（方案一），小丰同学沿矩形的对角线AC折出∠CAE=∠CAD，∠ACF=∠ACB的方法得到菱形AECF（方案二）.谁折出的菱形面积更大？请你通过计算说明.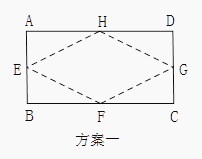
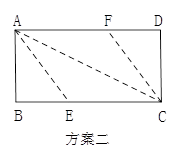
23. 菱形ABCD中，对角线AC和BD相交于O，已知AC=8，BD=6，求AB边上的高.
24.如图，在菱形ABCD中，∠A＝110°，E ， F分别是边AB和BC的中点，EP⊥CD于点P ， 求∠FPC ．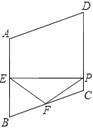
25. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF，已知BF＝8，DF＝4，求CD的长．
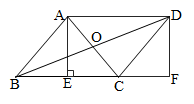26. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作 ，且 ，连接 ，连接 交 于点F.
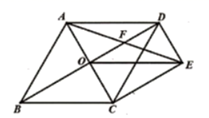(1)、求证： ；(2)、若菱形ABCD的边长为4， ，求 的长.27. 如图，在菱形ABCD中，∠A＝60°，E为菱形ABCD内对角线BD左侧一点，连接BE、CE、DE.
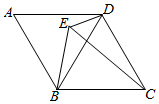(1)、若AB＝6，求菱形ABCD的面积；(2)、若∠BED＝2∠A，求证：CE＝BE+DE.28. 如图，在矩形ABCD中，AC＝60 cm ， ∠BAC＝60°，点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，同时点F从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点E ， F运动的时间是t秒(0<t≤15)．过点F作OF⊥BC于点O ， 连接OE ， EF.
(1)、求证：AE＝OF；(2)、四边形AEOF能够成为菱形吗？如果能，求出相应的t值，如果不能，请说明理由；(3)、当t为何值时，△OEF为直角三角形？请说明理由．