2016年湖北省十堰市中考数学试卷

试卷更新日期：2016-07-21 类型：中考真卷

进入出卷网下载

一、选择题．

1. $\frac{1}{2}$ 的倒数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下面几何体中，其主视图与俯视图相同的是（　　）

A、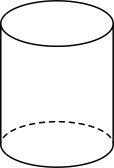 B、 C、 D、

查看试题解析
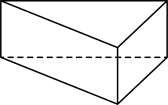
3. 一次数学测验中，某小组五位同学的成绩分别是：110，105，90，95，90，则这五个数据的中位数是（　　）

A、90 B、95 C、100 D、105

查看试题解析
4. 下列运算正确的是（　　）

A、a²•a³=a⁶ B、（﹣a³）²=﹣a⁶ C、（ab）²=ab² D、2a³÷a=2a²

查看试题解析
5.
如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB=3OB′，则△A′B′C′与△ABC的面积比为（　　）

A、1：3 B、1：4 C、1：5 D、1：9

查看试题解析
6.
如图，AB∥EF，CD⊥EF于点D，若∠ABC=40°，则∠BCD=（　　）

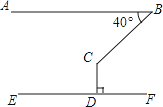A、140° B、130° C、120° D、110°

查看试题解析
7. 用换元法解方程 $\frac{x^{2} - 12}{x}$ ﹣ $\frac{4 x}{x^{2} - 12}$ =3时，设 $\frac{x^{2} - 12}{x}$ =y，则原方程可化为（　　）

A、y= $\frac{1}{y}$ ﹣3=0 B、y﹣ $\frac{4}{y}$ ﹣3=0 C、y﹣ $\frac{1}{y}$ +3=0 D、y﹣ $\frac{4}{y}$ +3=0

查看试题解析
8.
如图所示，小华从A点出发，沿直线前进10米后左转24，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地A点时，一共走的路程是（　　）

A、140米 B、150米 C、160米 D、240米

查看试题解析
9.
如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（　　）

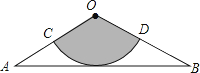A、10cm B、15cm C、10 $\sqrt{3}$ cm D、20 $\sqrt{2}$ cm

查看试题解析
10.
如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y= $\frac{k}{x}$ 上（k＞0，x＞0），则k的值为（　　）

A、25 $\sqrt{3}$ B、18 $\sqrt{3}$ C、9 $\sqrt{3}$ D、9

查看试题解析

二、填空题．

11. 武当山机场于2016年2月5日正式通航以来，截至5月底，旅客吞吐近92000人次，92000用科学记数法表示为．

查看试题解析
12. 计算：| $\sqrt[3]{8}$ ﹣4|﹣（ $\frac{1}{2}$ ）^﹣²= ．

查看试题解析
13. 某种药品原来售价100元，连续两次降价后售价为81元，若每次下降的百分率相同，则这个百分率是．

查看试题解析
14.
如图，在▱ABCD中，AB=2 $\sqrt{13}$ cm，AD=4cm，AC⊥BC，则△DBC比△ABC的周长长cm．

查看试题解析
15.
在综合实践课上，小聪所在小组要测量一条河的宽度，如图，河岸EF∥MN，小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向，然后沿河岸走了30米，到达B处，测得河对岸电线杆D位于北偏东30°方向，此时，其他同学测得CD=10米．请根据这些数据求出河的宽度为米．（结果保留根号）

查看试题解析
16. 已知关于x的二次函数y=ax²+bx+c的图象经过点（﹣2，y₁），（﹣1，y₂），（1，0），且y₁＜0＜y₂ ，对于以下结论：
①abc＞0；②a+3b+2c≤0；③对于自变量x的任意一个取值，都有 $\frac{a}{b}$ x²+x≥﹣ $\frac{b}{4 a}$ ；④在﹣2＜x＜﹣1中存在一个实数x₀ ，使得x₀=﹣ $\frac{a + b}{a}$ ，
其中结论错误的是（只填写序号）．

查看试题解析

三、解答题．

17. 化简： $\frac{x^{2} - 4 x + 4}{x^{2} - 4} + \frac{x - 2}{x^{2} + 2 x} + 2$ ．

查看试题解析
18. x取哪些整数值时，不等式5x+2＞3（x﹣1）与 $\frac{1}{2}$ x≤2﹣ $\frac{3 x}{2}$ 都成立？

查看试题解析
19.
如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF．

查看试题解析
20.
为了提高科技创新意识，我市某中学在“2016年科技节”活动中举行科技比赛，包括“航模”、“机器人”、“环保”、“建模”四个类别（每个学生只能参加一个类别的比赛），各类别参赛人数统计如图：

请根据以上信息，解答下列问题：

(1)、全体参赛的学生共有人，“建模”在扇形统计图中的圆心角是°；

(2)、将条形统计图补充完整；

(3)、在比赛结果中，获得“环保”类一等奖的学生为1名男生和2名女生，获得“建模”类一等奖的学生为1名男生和1名女生，现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动，问选取的两人中恰为1男生1女生的概率是多少？

查看试题解析
21. 已知关于x的方程（x﹣3）（x﹣2）﹣p²=0．

(1)、求证：无论p取何值时，方程总有两个不相等的实数根；

(2)、设方程两实数根分别为x₁ ， x₂ ，且满足 $x_{1}^{2} + x_{2}^{2} = 3 x_{1} x_{2}$ ，求实数p的值．

查看试题解析
22. 一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg，销售单价不低于120元/kg．且不高于180元/kg，经销一段时间后得到如下数据：
销售单价x（元/kg）
120
130
…
180
每天销量y（kg）
100
95
…
70
设y与x的关系是我们所学过的某一种函数关系．

(1)、直接写出y与x的函数关系式，并指出自变量x的取值范围；

(2)、当销售单价为多少时，销售利润最大？最大利润是多少？

查看试题解析
23.
如图，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F．

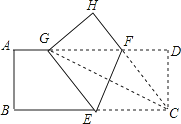(1)、判断四边形CEGF的形状，并证明你的结论；

(2)、若AB=3，BC=9，求线段CE的取值范围．

查看试题解析
24.
如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．

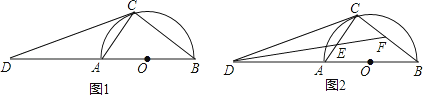(1)、求证：∠ACD=∠B；

(2)、
如图2，∠BDC的平分线分别交AC，BC于点E，F；
①求tan∠CFE的值；
②若AC=3，BC=4，求CE的长．

查看试题解析
25.
如图1，在平面直角坐标系xOy中，抛物线y=ax²+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．

(1)、求抛物线的解析式，并写出其顶点B的坐标；

(2)、①当P点运动到A点处时，计算：PO= ， PH= ，由此发现，POPH（填“＞”、“＜”或“=”）；
②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；

(3)、
如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．

查看试题解析

销售单价x（元/kg）	120	130	…	180
每天销量y（kg）	100	95	…	70