2016年贵州省毕节地区中考数学试卷
试卷更新日期:2016-07-21 类型:中考真卷
一、选择题
-
1. 的算术平方根是( )
A、2 B、±2 C、 D、±2. 2016年5月下旬,中国大数据博览会在贵阳举行,参加此次大会的人数约有89000人,将89000用科学记数法表示为( )A、89×103 B、8.9×104 C、8.9×103 D、0.89×1053. 下列运算正确的是( )A、﹣2(a+b)=﹣2a+2b B、(a2)3=a5 C、a3+4a= a3 D、3a2•2a3=6a54.图中是一个少数民族手鼓的轮廓图,其主视图是( )
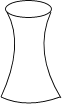 A、
A、 B、
B、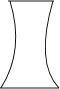 C、
C、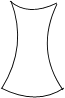 D、
D、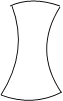 5. 为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,这四组数据的众数是( )
5. 为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,这四组数据的众数是( )
A、52和54 B、52 C、53 D、546. 到三角形三个顶点的距离都相等的点是这个三角形的( )A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点7. 估计的值在A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间8.如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )
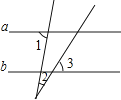 A、85° B、60° C、50° D、35°9. 已知关于x,y的方程x2m﹣n﹣2+4ym+n+1=6是二元一次方程,则m,n的值为( )A、m=1,n=﹣1 B、m=﹣1,n=1 C、 D、10. 如图,点A为反比例函数 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A、85° B、60° C、50° D、35°9. 已知关于x,y的方程x2m﹣n﹣2+4ym+n+1=6是二元一次方程,则m,n的值为( )A、m=1,n=﹣1 B、m=﹣1,n=1 C、 D、10. 如图,点A为反比例函数 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )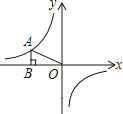 A、﹣4 B、4 C、﹣2 D、211. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线相等 D、平行四边形是轴对称图形12.
A、﹣4 B、4 C、﹣2 D、211. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线相等 D、平行四边形是轴对称图形12.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
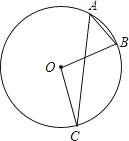 A、100° B、72° C、64° D、36°13. 为加快“最美毕节”环境建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树30棵,现在植树400棵所需时间与原计划植树300棵所需时间相同,设现在平均每天植树x棵,则列出的方程为( )A、 B、 C、 D、14. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、100° B、72° C、64° D、36°13. 为加快“最美毕节”环境建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树30棵,现在植树400棵所需时间与原计划植树300棵所需时间相同,设现在平均每天植树x棵,则列出的方程为( )A、 B、 C、 D、14. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、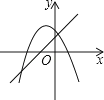 B、
B、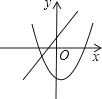 C、
C、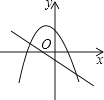 D、
D、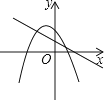 15. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
15. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )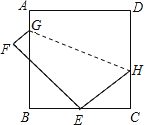 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
16. 分解因式3m4﹣48= .17. 若a2+5ab﹣b2=0,则 的值为 .18. 掷两枚质地均匀的骰子,其点数之和大于10的概率为 .
19. 在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC= ,AB=3,则BD= .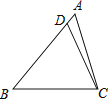 20. 如图,分别以边长等于1的正方形的四边为直径作半圆,则图中阴影部分的面积为
20. 如图,分别以边长等于1的正方形的四边为直径作半圆,则图中阴影部分的面积为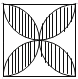
三、解答题
-
21. 计算: .22. 已知
(1)、化简A;(2)、若x满足不等式组 ,且x为整数时,求A的值.23. 为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)、求这两年该县投入教育经费的年平均增长率;
(2)、若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.24. 为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:组别
成绩x(分)
频数(人数)
频率
一
50≤x<60
2
0.04
二
60≤x<70
10
0.2
三
70≤x<80
14
b
四
80≤x<90
a
0.32
五
90≤x<100
8
0.16
请根据表格提供的信息,解答以下问题:
(1)、本次决赛共有名学生参加;
(2)、直接写出表中a= , b=;(3)、请补全下面相应的频数分布直方图;
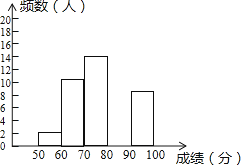 (4)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .25. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(4)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .25. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.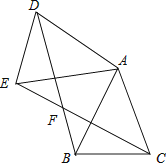 (1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.26. 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
(1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.26. 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.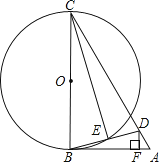 (1)、求证:AB是⊙O的切线;(2)、若∠A=60°,DF= ,求⊙O的直径BC的长.
(1)、求证:AB是⊙O的切线;(2)、若∠A=60°,DF= ,求⊙O的直径BC的长.
27. 如图,已知抛物线y=x2+bx与直线y=2x+4交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作x轴、y轴的平行线与直线AB交于点C和点E.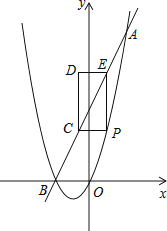 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、若C为AB中点,求PC的长;(3)、如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式.