2016年广东省茂名市中考数学试卷
试卷更新日期:2016-07-21 类型:中考真卷
一、选择题
-
1. 2016的相反数是( )A、﹣2016 B、2016 C、﹣ D、2. 2015年茂名市生产总值约2450亿元,将2450用科学记数法表示为( )A、0.245×104 B、2.45×103 C、24.5×102 D、2.45×10113.
如图是某几何体的三视图,该几何体是( )
 A、球 B、三棱柱 C、圆柱 D、圆锥4. 下列事件中,是必然事件的是( )A、两条线段可以组成一个三角形 B、400人中有两个人的生日在同一天 C、早上的太阳从西方升起 D、打开电视机,它正在播放动画片5.
A、球 B、三棱柱 C、圆柱 D、圆锥4. 下列事件中,是必然事件的是( )A、两条线段可以组成一个三角形 B、400人中有两个人的生日在同一天 C、早上的太阳从西方升起 D、打开电视机,它正在播放动画片5.如图,直线a、b被直线c所截,若a∥b,∠1=60°,那么∠2的度数为( )
 A、120° B、90° C、60° D、30°6. 下列各式计算正确的是( )
A、120° B、90° C、60° D、30°6. 下列各式计算正确的是( )
A、a2•a3=a6 B、(a2)3=a5 C、a2+3a2=4a4 D、a4÷a2=a27. 下列说法正确的是( )
A、长方体的截面一定是长方形 B、了解一批日光灯的使用寿命适合采用的调查方式是普查 C、一个圆形和它平移后所得的圆形全等 D、多边形的外角和不一定都等于360°8. 不等式组 的解集在数轴上表示为( )
A、 B、
B、 C、
C、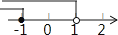 D、
D、 9.
9.如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
 A、150° B、140° C、130° D、120°10. 我国古代数学名著《孙子算经》中记载了一道题,大意是:求100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、
A、150° B、140° C、130° D、120°10. 我国古代数学名著《孙子算经》中记载了一道题,大意是:求100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、二、填空题
-
11. 一组数据2、4、5、6、8的中位数是 .
12. 已知∠A=100°,那么∠A补角为度.13. 因式分解:x2﹣2x= .14.已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD= .
 15.
15.如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .

三、解答题(共10小题,满分75分)
-
16. 计算:(﹣1)2016+ ﹣|﹣ |﹣(π﹣3.14)0 .17. 先化简,再求值:x(x﹣2)+(x+1)2 , 其中x=1.
18.某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.

求证:AB=CD,
(1)、补全求证部分;(2)、请你写出证明过程.19.为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
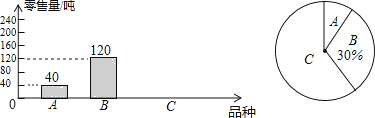 (1)、该市场6月上半月共销售这三种荔枝多少吨?(2)、该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?20. 有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.(1)、随机抽取一张卡片,求抽到数字“2”的概率;(2)、随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“1”且第二次抽到数字“2”的概率.21.
(1)、该市场6月上半月共销售这三种荔枝多少吨?(2)、该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?20. 有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.(1)、随机抽取一张卡片,求抽到数字“2”的概率;(2)、随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“1”且第二次抽到数字“2”的概率.21.如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
 (1)、求教学楼与旗杆的水平距离AD;(结果保留根号)(2)、求旗杆CD的高度.22.
(1)、求教学楼与旗杆的水平距离AD;(结果保留根号)(2)、求旗杆CD的高度.22.如图,一次函数y=x+b的图象与反比例函数y= (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
 (1)、求反比例函数的表达式和a、b的值;(2)、若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.23. 某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
(1)、求反比例函数的表达式和a、b的值;(2)、若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.23. 某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:“读书节”活动计划书
书本类别
A类
B类
进价(单位:元)
18
12
备注
1、用不超过16800元购进A、B两类图书共1000本;
2、A类图书不少于600本;
…
(1)、陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;(2)、经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?24.如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE= ∠A.
 (1)、求证:BC是⊙O的切线;(2)、若sinB= ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).25.
(1)、求证:BC是⊙O的切线;(2)、若sinB= ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).25.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
 (1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点P是线段BD上一点,当PE=PC时,求点P的坐标;(3)、在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
(1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点P是线段BD上一点,当PE=PC时,求点P的坐标;(3)、在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.