初中数学苏科版八年级下册 9.3 平行四边形的性质 同步训练
试卷更新日期：2021-03-17 类型：同步测试
一、单选题
-
1. 平行四边形不一定具有的性质是（ ）A、对角线互相平分 B、对边平行 C、对角线互相垂直 D、对边相等2. 在 中， ，则 的度数是 （ ）A、 B、 C、 D、3. 如图，在 ABCD 中，对角线 AC，BD 相交于点 O，下列结论一定成立的是（ ）
A、AC=BC B、AO=OC C、 D、4. 如图，在平行四边形ABCD中，CE平分∠BCD交AD于点E，已知AE=2，ED=4，则平行四边形ABCD的周长为（ ）
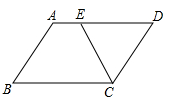A、16 B、18 C、20 D、225. 如图，在▱ABCD中，CE⊥AB，E为垂足.如果∠A=120°，∠BCE的度数为( )
A、20° B、30° C、40° D、60°6. 如图，四边形ABCD中，AB∥CD，BC∥AD，点E、F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（ ）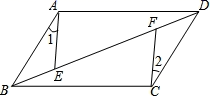
A、∠1=∠2 B、BF=DE C、AE=CF D、∠AED=∠CFB7. 如图，在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上一点E，且BE＝4，CE＝3.则AD的长是（ ）
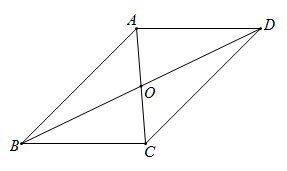
A、3 B、4 C、5 D、2.58. 在平行四边形ABCD中， ，对角线AC的垂直平分线交AD于点E，连接CE若平行四边形ABCD的周长为20cm，则 的周长为（ ）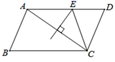
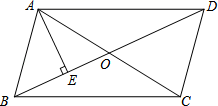
A、20cm B、40cm C、15cm D、10cm9. 如图所示，在直角坐标系内，原点O恰好是▱ABCD对角线的交点，若A点坐标为（2，3），则C点坐标为（ ）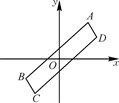
A、（－3，－2） B、（－2，3） C、（－2，－3） D、（2，－3）10. 如图， 的对角线 交于点 平分 交 于点 连接 .下列结论： ； 平分 ； ； ，其中正确的有（ ）
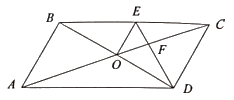A、 个 B、 个 C、 个 D、 个二、填空题
-
11. 在▱ABCD中，AB：BC=4：3，周长为28cm，则AD=cm．12. 在平面直角坐标系中，点A、B、C的坐标分别是 ， ， ，若以点A、B、C、D为顶点的四边形是平行四边形，则满足条件的D点共有个.13. 如图，在平行四边形ABCD中，按以下步骤作图：①以点A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以点M，N为圆心，以大于 MN的长为半径作弧，两弧相交于点P；③作射线AP交CD于点Q.若DQ＝2QC，BC＝3，则平行四边形ABCD的周长为.
14. 如图，在平行四边形ABCD中，DE平分∠ADC，AD＝7，BE＝2，则平行四边形ABCD的周长是 ．
15. 如图， 中， 和 的平分线分别交 于E、F两点， 、 交与点G，若 ， ，则 .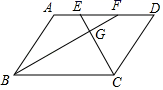
16. 如图，将 ABCD沿对角线AC折叠，使点B落在点B'处.若∠1=∠2=42°，则∠B为°.
17. 如图，已知▱ABCO的顶点A、C分别在直线x＝2和x＝7上，O是坐标原点，则对角线OB长的最小值为.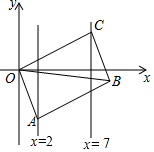
18. 如图，▱ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝ BC，连结OE.下列结论：①∠CAD＝30°；②S▱ABCD＝AB·AC；③OB＝AB；④OE＝ BC，成立的结论有 ． (填序号)
三、解答题
-
19. 如图，点E，F为▱ABCD的对角线BD上的两点，连接AE，CF，∠AEB＝∠CFD.求证：AE＝CF.
20. 如图，平行四边形ABCD的对角线AC，BD相交于点O，E、F分别是OA、OC的中点.求证：BE＝DF
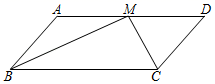
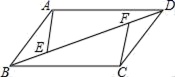
21. 如图，E是▱ABCD的边AB的中点，连接CE并延长交DA的延长线于F，若BC＝8，求DF的长．
22. 如图，E，F是平行四边形ABCD的对角线AC上的点，CE＝AF.请你猜想：BE与DF有怎样的位置关系和数量关系？并对你的猜想加以证明.
23. 如图，在平行四边形ABCD中，E、F为对角线BD上的两点，且∠BAF＝∠DCE．求证：BE＝DF．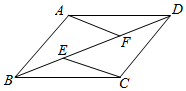
24. 如图，已知E、F是▱ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.
(1)、请写出图中全等三角形（不再添加辅助线）．(2)、求证：△ABE≌△CDF；25. 如图所示，已知点E，F在 ABCD的对角线BD上，且BE=DF.
求证：
(1)、△ABE≌△CDF；(2)、AE∥CF.
