初中数学苏科版八年级下册 9.2 中心对称与中心对称图形 同步训练
试卷更新日期：2021-03-17 类型：同步测试
一、单选题
-
1. 下列图形中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 在正三角形、等腰梯形、矩形和圆这四种图形中，既是轴对称图形又是中心对称图形的有（ ）种．
A、1 B、2 C、3 D、43. 下列说法正确的是（ ）A、全等的两个图形成中心对称 B、成中心对称的两个图形必须重合 C、成中心对称的两个图形全等 D、旋转后能够重合的两个图形成中心对称4. 如图，已知图形是中心对称图形，则对称中心是（ ）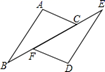
A、点C B、点D C、线段BC的中点 D、线段FC的中点5. 已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称，则AB与A′B′的关系是（ ）A、相等 B、垂直 C、相等并且平行 D、相等并且平行或相等并且在同一直线上6. 如图，四边形ABD与四边形FGHE关于一个点成中心对称，则这个点是（ ）
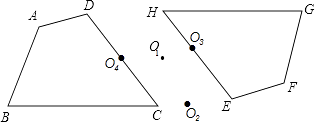A、O1 B、O2 C、O3 D、O47. 已知△ABC和△DEF关于点O对称，相应的对称点如图所示，则下列结论正确的是（ ）
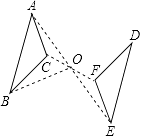A、AO=BO B、BO=EO C、点A关于点O的对称点是点D D、点D 在BO的延长线上8. 如图，在方格纸中，选择标有序号①②③④的小正方形中的一个涂黑，
与图中阴影部分构成中心对称图形，则该小正方形的序号是（ ）
A、① B、② C、③ D、④9. 四张扑克牌如图①所示放在桌面上，小敏把其中一张旋转180°后得到图②，则她所旋转的牌从左数起是（ ）
A、第一张 B、第二张 C、第三张 D、第四张10. 若两个图形成中心对称，则下列说法：①对应点的连线必经过对称中心；②这两个图形的形状大小完全相同；③这两个图形的对应线段一定相等；④将一个图形绕对称中心旋转180°后必与另一个图形重合．正确的有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 请写出一个是中心对称图形的几何图形的名称：
12. 六张完全相同的卡片上，分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形，现从中随机抽取一张，卡片上画的恰好既是轴对称图形又是中心对称图形的概率为 ．13. 如图，如果△ABC和△DEF关于点G成中心对称，那么△ABC绕点G旋转°后能与△DEF重合.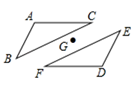
14. 如图是一个中心对称图形，A为对称中心，若∠C＝90°，∠B＝30°，AC＝1，则BB′的长为.
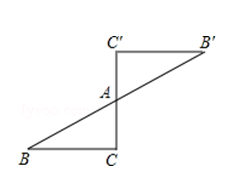15. 如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB=3，OD=2，则阴影部分的面积之和为 ．
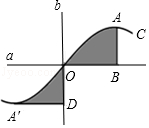16. 下列说法：①成中心对称的两个图形全等；
②图形的旋转不改变图形的形状、大小；
③成中心对称的两个图形，对称点的连线被对称中心平分，
其中正确的个数为 .
17.在平面直角坐标系中，点P（1，1），N（2，0），△MNP和△M1N1P1的顶点都在格点上，△MNP与△M1N1P1是关于某一点中心对称，则对称中心的坐标为 .
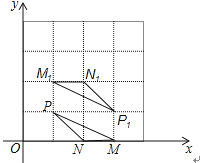18.将五个边长都为3cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和是 cm2 ．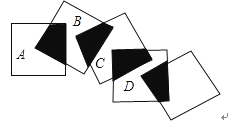
三、解答题
-
19. 如图，△ABC与△DEF关于点O对称，请你写出两个三角形中的对称点，相等的线段，相等的角．
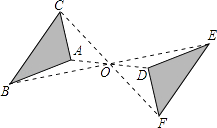20. 用直尺和圆规作图：已知△ABC与△A'B'C'成中心对称（点A与A'对应，点B与B'对应），请在图中画出对称中心O，并画出完整的△A'B'C'．（保留作图痕迹）
21. 由16个边长相等的小正方形组成的图形如图所示，请你用一条割线（可以是折线）将它分割成两个图形，使之关于某一点成中心对称，要求给出两种不同的方法．
22. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）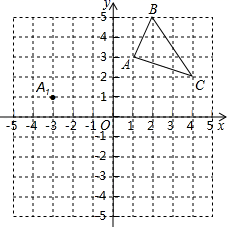
（ 1 ）将△ABC平移，使点A移动到点A1 ， 请画出△A1B1C1；
（ 2 ）作出△ABC关于O点成中心对称的△A2B2C2 ， 并直接写出A2 ， B2 ， C2的坐标；
（ 3 ）△A1B1C1与△A2B2C2是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由.
23.如图是由两个矩形组成的组合图形，能否在图形中找到一点P，沿过点P的某一条直线折叠该图形，能将该图形分成面积相等的两部分？若能，请你在图中做出点P，并说明点P的位置；若不能，请说明理由．
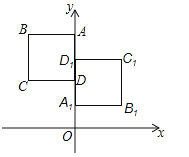
24.如图，正方形ABCD于正方形A1B1C1D1关于某点中心对称，已知A，D1 ， D三点的坐标分别是（0，4），（0，3），（0，2）．
（1）求对称中心的坐标．
（2）写出顶点B，C，B1 ， C1的坐标．
25.如图，由4个全等的正方形组成的L形图案，请按下列要求画图：
(1)、在图案①中添加1个正方形，使它成轴对称图形（不能是中心对称图形）；(2)、在图案②中添画1个正方形，使它成中心对称图形（不能是轴对称图形）；(3)、在图案中改变1个正方形的位置，画成图案③，使它既成中心对称图形，又成轴对称图形．26.课外兴趣小组活动时，老师提出了如下问题：
(1)、如图1，在△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．
[感悟]解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
(2)、解决问题：受到（1）的启发，请你证明下列命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．求证：BE+CF＞EF，若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明．