初中数学苏科版八年级下册 9.1 图形的旋转 同步训练
试卷更新日期:2021-03-17 类型:同步测试
一、单选题
-
1. 在绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在图形旋转中,下列说法错误的是( )A、旋转中心到对应点的距离相等 B、图形上的每一点转动的角度相同 C、图形上可能存在不动点 D、图形上任意两点的连线与其对应两点的连线相等3. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若BE=17,AD=7,则BC为( )
2. 在图形旋转中,下列说法错误的是( )A、旋转中心到对应点的距离相等 B、图形上的每一点转动的角度相同 C、图形上可能存在不动点 D、图形上任意两点的连线与其对应两点的连线相等3. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若BE=17,AD=7,则BC为( )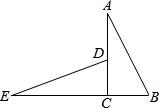 A、3 B、4 C、5 D、64. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )
A、3 B、4 C、5 D、64. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )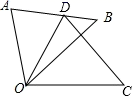 A、 B、 C、 D、5. 如图,点A,B,C,D,O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得:则旋转的角度为( )
A、 B、 C、 D、5. 如图,点A,B,C,D,O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得:则旋转的角度为( )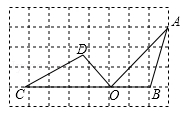 A、30° B、45° C、90° D、135°6. 如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转 60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在 OB上),则∠A′CO的度数为( )
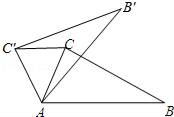
A、30° B、45° C、90° D、135°6. 如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转 60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在 OB上),则∠A′CO的度数为( )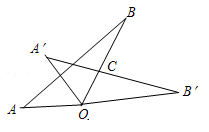 A、85° B、75° C、95° D、105°7. 如图,把 绕点A逆时针旋转40°,得到 ,点 恰好落在边AB上,连接 ,则 的度数为( )
A、85° B、75° C、95° D、105°7. 如图,把 绕点A逆时针旋转40°,得到 ,点 恰好落在边AB上,连接 ,则 的度数为( )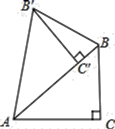 A、15° B、20° C、25° D、30°8. 如图,在 中, 将 绕点 顺时针方向旋转得到 当点 的对应点 恰好落在 边上时,则 的长为( )
A、15° B、20° C、25° D、30°8. 如图,在 中, 将 绕点 顺时针方向旋转得到 当点 的对应点 恰好落在 边上时,则 的长为( )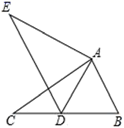 A、 B、 C、 D、9. 如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )
A、 B、 C、 D、9. 如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )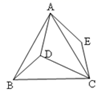 A、12 B、 C、 D、10. 如图,O是正 内一点, , , ,将线段BO以点B为旋转中心逆时针旋转 得到线段 ,下列五个结论中,其中正确的结论是( )
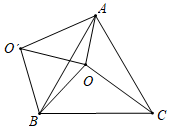
A、12 B、 C、 D、10. 如图,O是正 内一点, , , ,将线段BO以点B为旋转中心逆时针旋转 得到线段 ,下列五个结论中,其中正确的结论是( )可以由 绕点B逆时针旋转 得到; 点O与 的距离为4; ; ; .
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一个正三角形至少绕其中心旋转度,就能与其自身重合.12. 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠B′AB等于.
 13. 如图,将△ABC绕点C按逆时针方向旋转得到△DEC,使D点落在AB上,若∠CAB=66°,则∠BCE的大小是°.
13. 如图,将△ABC绕点C按逆时针方向旋转得到△DEC,使D点落在AB上,若∠CAB=66°,则∠BCE的大小是°.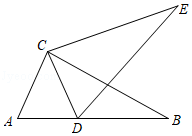 14. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是.
14. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是.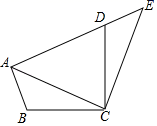 15. 如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .
15. 如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .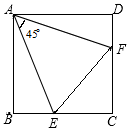 16. 如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为.
16. 如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为.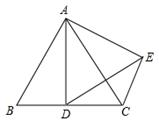 17. 如图, 中, , , , 是 内部的任意一点,连接 , , ,则 的最小值为 .
17. 如图, 中, , , , 是 内部的任意一点,连接 , , ,则 的最小值为 .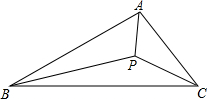
三、解答题
-
18. △ABC在平面直角坐标系中的位置如图所示.
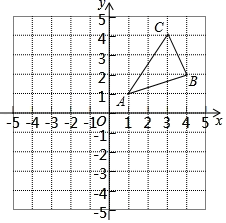 (1)、将△ABC向左平移4个单位长度后得到△A1B1C1 , 点A1、B1、C1分别是A、B、C的对应点,请画出△A1B1C1 , 并写出C1的坐标;(2)、将△ABC绕点O顺时针旋转90°,得到△A2B2C2 , 点A2、B2、C2分别是A、B、C的对应点,请画出△A1B1C1 , 并写出C2的坐标.19. 如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1 , 点A与点A1 , 点B与点B1 , 点C与点C1是对应点.
(1)、将△ABC向左平移4个单位长度后得到△A1B1C1 , 点A1、B1、C1分别是A、B、C的对应点,请画出△A1B1C1 , 并写出C1的坐标;(2)、将△ABC绕点O顺时针旋转90°,得到△A2B2C2 , 点A2、B2、C2分别是A、B、C的对应点,请画出△A1B1C1 , 并写出C2的坐标.19. 如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1 , 点A与点A1 , 点B与点B1 , 点C与点C1是对应点.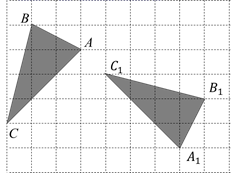 (1)、请通过画图找到旋转中心,将其标记为点O;(2)、直接写出旋转角α的度数.20. 已知AD⊥AB于A,BE⊥AB于B,点C在线段AB上,DC⊥EC,且DC=CE.
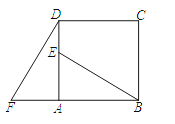
(1)、请通过画图找到旋转中心,将其标记为点O;(2)、直接写出旋转角α的度数.20. 已知AD⊥AB于A,BE⊥AB于B,点C在线段AB上,DC⊥EC,且DC=CE. (1)、求证:AD+BE=AB;(2)、将△BEC绕点C逆时针旋转,使点B落在AC上,如图(2),试问:AD,BE,AB又怎样的数量关系?说明理由.21. 如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)、求证:AD+BE=AB;(2)、将△BEC绕点C逆时针旋转,使点B落在AC上,如图(2),试问:AD,BE,AB又怎样的数量关系?说明理由.21. 如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?
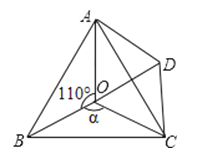
 22. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
22. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
 23. 如图,点O是等边三角形ABC内的一点, ,将三角形 绕点C按顺时针旋转得到 ,连接OD,OA
23. 如图,点O是等边三角形ABC内的一点, ,将三角形 绕点C按顺时针旋转得到 ,连接OD,OA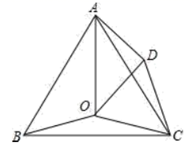 (1)、求 的度数;(2)、若 , ,求三角形ADO的面积.24. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
(1)、求 的度数;(2)、若 , ,求三角形ADO的面积.24. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.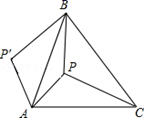 (1)、求点P与点P′之间的距离;(2)、求∠APB的度数.25. 如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.
(1)、求点P与点P′之间的距离;(2)、求∠APB的度数.25. 如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.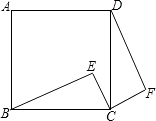 (1)、请问最小旋转度数为多少?
(1)、请问最小旋转度数为多少?
(2)、指出图中的全等图形以及它们的对应角?
(3)、若∠EBC=30°,∠BCE=80°,求∠F的度数.26. 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.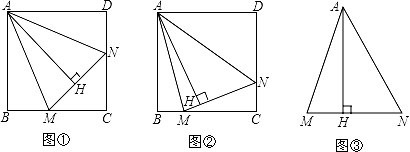 (1)、如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)、如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)、如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)27. 某数学活动小组在一次活动中,对一个数学问题作如下研究:
(1)、如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)、如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)、如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)27. 某数学活动小组在一次活动中,对一个数学问题作如下研究: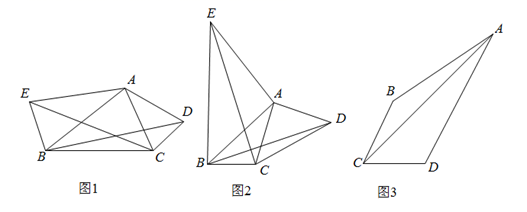 (1)、(问题呈现)
(1)、(问题呈现)如图1, 中分别以 为边向外作等腰 和等腰 ,使 , , ,连结 ,试猜想 与 的大小关系,并说明理由.
(2)、(问题再探)如图2, 中分别以 为边向外作等腰 和等腰 , ,连结 ,若 ,求 的长.
(3)、(问题拓展)如图3,四边形 中,连结 , , , , , ,请直接写出 的长.