2016年宁夏中考数学试卷

试卷更新日期：2016-07-21 类型：中考真卷

进入出卷网下载

一、选择题

1. 某地一天的最高气温是8℃，最低气温是﹣2℃，则该地这天的温差是（）

A、10℃ B、﹣10℃ C、6℃ D、﹣6℃

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{a}$ + $\sqrt{b}$ = $\sqrt{a b}$ B、（﹣a²）²=﹣a⁴ C、（a﹣2）²=a²﹣4 D、 $\sqrt{a}$ ÷ $\sqrt{b}$ = $\sqrt{\frac{a}{b}}$ （a≥0，b＞0）

查看试题解析
3. 已知x，y满足方程组 ${\begin{cases} x + 6 y = 12 \\ 3 x - 2 y = 8 \end{cases}$ ，则x+y的值为（）

A、9 B、7 C、5 D、3

查看试题解析
4.
为响应“书香校响园”建设的号召，在全校形成良好的阅读氛围，随机调查了部分学生平均每天阅读时间，统计结果如图所示，则本次调查中阅读时间为的众数和中位数分别是（）

A、2和1 B、1.25和1 C、1和1 D、1和1.25

查看试题解析
5.
菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF= $\sqrt{2}$ ，BD=2，则菱形ABCD的面积为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、6 $\sqrt{2}$ D、8 $\sqrt{2}$

查看试题解析
6.
由若干个相同的小正方体组合而成的一个几何体的三视图如图所示，则组成这个几何体的小正方形个数是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛，选拔中每名学生的平均成绩 $\bar{x}$ 及其方差s²如表所示，如果要选拔一名成绩高且发挥稳定的学生参赛，则应选择的学生是（）

甲
乙
丙
丁
$\bar{x}$
8.9
9.5
9.5
8.9
s²
0.92
0.92
1.01
1.03

A、甲 B、乙 C、丙 D、丁

查看试题解析
8.
正比例函数y₁=k₁x的图象与反比例函数y₂= $\frac{k_{2}}{x}$ 的图象相交于A，B两点，其中点B的横坐标为﹣2，当y₁＜y₂时，x的取值范围是（）

A、x＜﹣2或x＞2 B、x＜﹣2或0＜x＜2 C、﹣2＜x＜0或0＜x＜2 D、﹣2＜x＜0或x＞2

查看试题解析

二、填空题

9. 分解因式：mn²﹣m= ．

查看试题解析
10. 若二次函数y=x²﹣2x+m的图象与x轴有两个交点，则m的取值范围是．

查看试题解析
11.
实数a在数轴上的位置如图，则|a﹣3|= ．

查看试题解析
12. 用一个圆心角为180°，半径为4的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径为．

查看试题解析
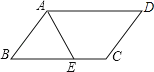
13.
在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于．

查看试题解析
14.
如图，Rt△AOB中，∠AOB=90°，OA在x轴上，OB在y轴上，点A，B的坐标分别为（ $\sqrt{3}$ ，0），（0，1），把Rt△AOB沿着AB对折得到Rt△AO′B，则点O′的坐标为．

查看试题解析
15. 已知正△ABC的边长为6，那么能够完全覆盖这个正△ABC的最小圆的半径是．

查看试题解析
16.
如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为．

查看试题解析

三、解答题（本题共6道题，每题6分，共36分）

17. 解不等式组 ${\begin{cases} x + 1 > \frac{3 x - 1}{2} \\ 2 x - (x - 3) \geq 5 \end{cases}$ ．

查看试题解析
18. 化简求值：（ $\frac{a}{a + 2} + \frac{1}{a^{2} - 4}$ ） $\div \frac{a - 1}{a + 2} + \frac{1}{a - 2}$ ，其中a=2+ $\sqrt{2}$ ．

查看试题解析
19.
在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣1），B（3，﹣3），C（0，﹣4）

(1)、画出△ABC关于原点O成中心对称的△A₁B₁C₁；

(2)、画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂ ．

查看试题解析
20. 为了解学生的体能情况，随机选取了1000名学生进行调查，并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况，整理成以下统计表，其中“√”表示喜欢，“×”表示不喜欢．
项目
学生
长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×

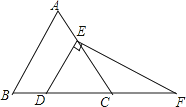
(1)、估计学生同时喜欢短跑和跳绳的概率；

(2)、估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率；

(3)、如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大？

查看试题解析
21.
在等边△ABC中，点D，E分别在边BC、AC上，若CD=2，过点D作DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，求EF的长．

查看试题解析
22. 某种型号油电混合动力汽车，从A地到B地燃油行驶纯燃油费用76元，从A地到B地用电行驶纯电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

(1)、求每行驶1千米纯用电的费用；

(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少用电行驶多少千米？

查看试题解析

四、解答题

23.
已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．

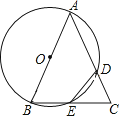(1)、求证：AB=AC；

(2)、若AB=4，BC=2 $\sqrt{3}$ ，求CD的长．

查看试题解析
24.
如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO=90°，∠AOB=30°，OB=2 $\sqrt{3}$ ，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过OA的中点C，交AB于点D．

(1)、求反比例函数的关系式；

(2)、连接CD，求四边形CDBO的面积．

查看试题解析
25.
某种水彩笔，在购买时，若同时额外购买笔芯，每个优惠价为3元，使用期间，若备用笔芯不足时需另外购买，每个5元．现要对在购买水彩笔时应同时购买几个笔芯作出选择，为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据，整理绘制出下面的条形统计图：
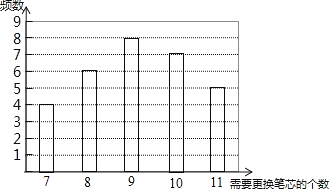
设x表示水彩笔在使用期内需要更换的笔芯个数，y表示每支水彩笔在购买笔芯上所需要的费用（单位：元），n表示购买水彩笔的同时购买的笔芯个数．

(1)、若n=9，求y与x的函数关系式；

(2)、若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5，确定n的最小值；

(3)、假设这30支笔在购买时，每支笔同时购买9个笔芯，或每支笔同时购买10个笔芯，分别计算这30支笔在购买笔芯所需费用的平均数，以费用最省作为选择依据，判断购买一支水彩笔的同时应购买9个还是10个笔芯．

查看试题解析
26.
在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：

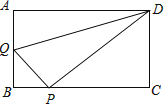(1)、设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；

(2)、是否存在x的值，使得QP⊥DP？试说明理由．

查看试题解析

项目学生	长跑	短跑	跳绳	跳远
200	√	×	√	√
300	×	√	×	√
150	√	√	√	×
200	√	×	√	×
150	√	×	×	×

	甲	乙	丙	丁
$\bar{x}$	8.9	9.5	9.5	8.9
s²	0.92	0.92	1.01	1.03