人教A版高中数学必修5 1.1 正弦定理和余弦定理
试卷更新日期:2021-03-17 类型:同步测试
一、单选题
-
1. 在 中,若 ,则 ( )A、30° B、45° C、60° D、120°2. 在 中,若 ,则角 ( )A、30°或60° B、45°或60° C、120°或60° D、30°或150°3. 已知 的内角 , , 的对边分别是 , , ,若 , , ,则 的面积为( )A、 B、 C、 D、4. 在 中,已知 , , ,则 的面积为( )A、 B、 C、 D、5. 在 中,设角A,B,C所对的边长分别为a,b,c, , , 的面积 ,则a等于( )A、 B、 C、 或 D、6. 在 中,若 , , ,则边 的长为( )A、 B、 C、 D、47. 在 中,角 的对边分别为 ,点D在边 上,已知 , ,则 ( )A、8 B、10 C、 D、8. 在 中,内角A,B,C所对边分别为a,b,c,若 , , 的面积为 ,则 ( )A、 B、 C、 D、
二、多选题
-
9. 在 中,角 所对的边分别为 a,b,c, ,a=2,若满足条件的三角形有且只有一个,则边b的可能取值为( )A、1 B、 C、2 D、310. 在 中,下列说法正确的是( )A、若 ,则 B、存在 满足 C、若 ,则 为钝角三角形 D、若 ,则11. 在 中,角 , , 所对的边分别为 , , ,且 ,则下列结论正确的是( )A、 B、 是钝角三角形 C、 的最大内角是最小内角的 倍 D、若 ,则 外接圆半径为12. 下列命题中,正确的是( )A、在 中, , B、在锐角 中,不等式 恒成立 C、在 中,若 ,则 必是等腰直角三角形 D、在 中,若 , ,则 必是等边三角形
三、填空题
-
13. 在 中,三个内角 、 、 的对边分别是 、 、 ,若 , , ,则 .14. 在 中,若 ,则 是三角形.15. 已知△ 中,角 所对的边分别为 , , ,且△ 的面积为 ,则 ; .16. 在 中,角 、 、 所对的边分别为 、 、 ,若满足 , 的 有且仅有一个,则边 的取值范围是.
四、解答题
-
17. 如图, 是直角 斜边 上一点, .
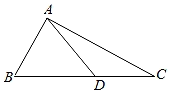 (1)、若 ,求角 的大小;(2)、若 ,且 求 的长.18. 在 中, , , 分别为内角 , , 所对的边,已知 ,其中 为 外接圆的半径.
(1)、若 ,求角 的大小;(2)、若 ,且 求 的长.18. 在 中, , , 分别为内角 , , 所对的边,已知 ,其中 为 外接圆的半径.(Ⅰ)求 ;
(Ⅱ)若 , ,求 的面积.
19. 在 C中,角A,B,C所对的边分别为a,b、c,已知 .(1)、求角C的大小;(2)、若 , 的面积为 ,分别求a+b、 的值.