2016年山东省潍坊市中考数学试卷
试卷更新日期:2016-07-21 类型:中考真卷
一、选择题:
-
1. 计算:20•2﹣3=( )
A、﹣ B、 C、-8 D、82. 下列科学计算器的按键中,其上面标注的符号是轴对称图形但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3.
3.如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
 A、
A、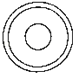 B、
B、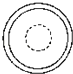 C、
C、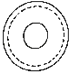 D、
D、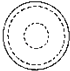 4. 近日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位)( )A、1.2×1011 B、1.3×1011 C、1.26×1011 D、0.13×10125.
4. 近日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位)( )A、1.2×1011 B、1.3×1011 C、1.26×1011 D、0.13×10125.实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )
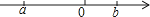 A、﹣2a+b B、2a﹣b C、﹣b D、b6. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )
A、﹣2a+b B、2a﹣b C、﹣b D、b6. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )
A、15° B、30° C、45° D、60°7. 木杆AB斜靠在墙壁上,当木杆的上端A沿墙壁NO竖直下滑时,木杆的底端B也随之沿着射线OM方向滑动.下列图中用虚线画出木杆中点P随之下落的路线,其中正确的是( )
A、 B、
B、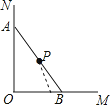 C、
C、 D、
D、 8. 将下列多项式因式分解,结果中不含有因式a+1的是( )
8. 将下列多项式因式分解,结果中不含有因式a+1的是( )
A、a2﹣1 B、a2+a C、a2+a﹣2 D、(a+2)2﹣2(a+2)+19.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
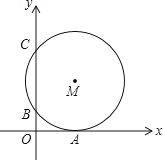 A、10 B、8 C、4 D、210. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
A、10 B、8 C、4 D、210. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣11.如图,在Rt△ABC中,∠A=30°,BC=2 ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
 A、﹣ B、﹣ C、﹣ D、﹣12.
A、﹣ B、﹣ C、﹣ D、﹣12.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
 A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23
A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23二、填空题:
-
13. 计算: ( + )= .
14. 若3x2nym与x4﹣nyn﹣1是同类项,则m+n= .
15. 超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:测试项目
创新能力
综合知识
语言表达
测试成绩(分数)
70
80
92
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是分.
16. 已知反比例函数y= (k≠0)的图象经过(3,﹣1),则当1<y<3时,自变量x的取值范围是 .
17. 已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是 .
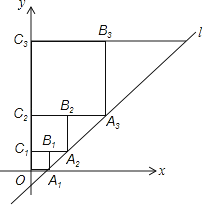
18.在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .
三、解答题:
-
19. 关于x的方程3x2+mx﹣8=0有一个根是 ,求另一个根及m的值.20.
今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分)
评定等级
频数
90≤n≤100
A
2
80≤n<90
B
70≤n<80
C
15
n<70
D
6
根据以上信息解答下列问题:
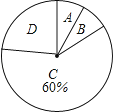 (1)、求m的值;(2)、在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)(3)、从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.21.
(1)、求m的值;(2)、在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)(3)、从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.21.正方形ABCD内接于⊙O,如图所示,在劣弧
 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: 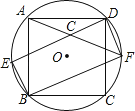 (1)、四边形EBFD是矩形;(2)、DG=BE.22.
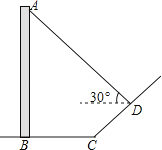
(1)、四边形EBFD是矩形;(2)、DG=BE.22.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
 23. 旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.(1)、优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)(2)、当每辆车的日租金为多少元时,每天的净收入最多?24.
23. 旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.(1)、优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)(2)、当每辆车的日租金为多少元时,每天的净收入最多?24.如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
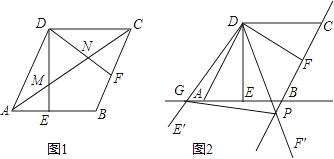 (1)、如图1,连接AC分别交DE、DF于点M、N,求证:MN= AC;(2)、如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 时,求旋转角的大小并指明旋转方向.25.
(1)、如图1,连接AC分别交DE、DF于点M、N,求证:MN= AC;(2)、如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 时,求旋转角的大小并指明旋转方向.25.如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.