湖北省宜昌市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 以下四张扑克牌的图案，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 将一元二次方程 $2 x^{2} - 1 = 3 x$ 化为一般形式后，其中二次项系数、一次项系数分别是（）

A、 $2, - 3$ B、 $- 2, - 3$ C、 $2, - 1$ D、 $- 2, - 1$

查看试题解析
3. 下列事件是不可能事件的是（）

A、任意画一个平行四边形，它是中心对称图形 B、李师傅买的彩票正好中奖 C、掷两次骰子，骰子的点数之积为14 D、翻开一本书，页码是奇数

查看试题解析
4. 若关于x的一元二次方程kx²+2x+1=0有实数根，则k的取值范围是（）

A、k≤1且k≠0 B、k≤1 C、k≥1 D、K<1且k≠0

查看试题解析
5. 在平面直角坐标系中，将点 $P (4, 3)$ 绕原点旋转 $180 °$ 后，得到对应点Q的坐标是（）

A、 $(4, - 3)$ B、 $(- 4, 3)$ C、 $(3, 4)$ D、 $(- 4, - 3)$

查看试题解析
6. 将函数 $y = x^{2} + 2 x + 1$ 的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数关系式是（）

A、 $y = {(x - 1)}^{2} + 2$ B、 $y = x^{2} + 2$ C、 $y = {(x + 1)}^{2} + 2$ D、 $y = x^{2} + x + 3$

查看试题解析
7. 一个密闭不透明的盒子里有若干个白球，在不许将球倒出来数的情况下，为了估计白球数，小刚向其中放入了8个黑球，搅匀后从中随意摸出一个球记下颜色，再把它放回盒中，不断重复这一过程，共摸球400次，其中80次摸到黑球，你估计盒中大约有白球（）

A、32个 B、36个 C、40个 D、42个

查看试题解析
8. 如图， $⊙ O$ 是四边形 $A B C D$ 的外接圆，若 $∠ B O D = 120^{\circ}$ ，则 $∠ C$ 的度数为（）

A、 $130^{\circ}$ B、 $120^{\circ}$ C、 $60^{\circ}$ D、 $150^{\circ}$

查看试题解析
9. 在某种病毒的传播过程中，每轮传染平均1人会传染x个人，若最初2个人感染该病毒，经过两轮传染，共有y人感染.则y与x的函数关系式为（）

A、 $y = 2 {(1 + x)}^{2}$ B、 $y = {(2 + x)}^{2}$ C、 $y = 2 + 2 x^{2}$ D、 $y = {(1 + 2 x)}^{2}$

查看试题解析
10. 如图，在 $Δ A B C$ 中， $∠ C A B = 70 °$ ，在同一平面内，将 $Δ A B C$ 绕点A旋转到 $△ A B' C^{'}$ 的位置，连接 $C C'$ .若 $C C' / / A B$ ，则 $∠ B A B^{'}$ 的度数为（）

A、 $30^{\circ}$ B、 $60^{\circ}$ C、 $40^{\circ}$ D、 $35^{\circ}$

查看试题解析
11. 如图，抛物线 $y_{1} = a x^{2} + b x + c$ 与直线 $y_{2} = k x + m$ 的交点为 $A (1 ， - 3) ， B (6 ， 1)$ .当 $y_{1} > y_{2}$ 时，x的取值范围是（）

A、 $1 < x < 6$ B、 $- 3 < x < 1$ C、 $x < - 3$ 或 $x > 1$ D、 $x < 1$ 或 $x > 6$

查看试题解析

二、填空题

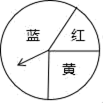
12. 如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°，90°，210°．让转盘自由转动，则指针停止后落在黄色区域的概率是．

查看试题解析
13. 已知 $x = 1$ 是关于x的一元二次方程 $x^{2} + 2 x + a = 0$ 的一个根，则a的值是.

查看试题解析
14. 如图，将 $R t Δ A B C$ 绕直角顶点A顺时针旋转一定角度得到 $R t Δ A D E$ ，点B的对应点D恰好落在 $B C$ 边上.若 $A B = 1 ， ∠ B = 60 °$ ，则 $C D$ 的长为.

查看试题解析
15. 若点 $A (- 2 ， y_{1}) ， B (2 ， y_{2})$ 在如图所示的抛物线上，则 $y_{1} ， y_{2}$ 的大小关系是.

查看试题解析

三、解答题

16. 解方程： $y^{2} + 6 y + 8 = 0$

查看试题解析
17. 已知，如图，扇形AOB的圆心角为120°，半径OA为6cm.

(1)、求扇形AOB的弧长和扇形面积；

(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒，求这个纸盒的高OH.

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中， $Δ A B C$ 的三个顶点坐标分别为 $A (2 ， 0) ， B (3 ， 1) ， C (1 ， 3)$ .

(1)、按下列要求画图；
①将 $Δ A B C$ 沿x轴向左平移 $2$ 个单位长度，得到 $Δ A_{1} B_{1} C_{1}$ ，请画出 $Δ A_{1} B_{1} C_{1}$ ；

②将 $Δ A_{1} B_{1} C_{1}$ 绕点O逆时针旋转 $90 °$ ，得到 $Δ A_{2} B_{2} C_{2}$ ，请画出 $Δ A_{2} B_{2} C_{2}$ .

(2)、 $Δ B C_{1} C_{2}$ 是三角形，其外接圆的半径 $R =$ .

查看试题解析
19. $901$ 班召开“美丽宜昌”主题班会，准备随机选取1名主持人和两名介绍宜昌风光的学生.班主任准备了“①号三峡大坝”、“②号三峡人家”、“③号清江画廊”、“④号三峡大瀑布”四处景点的照片各一张，并将它们背面朝上放置（照片背面完全相同）.

(1)、已知 $901$ 班共有 $40$ 名同学，请写出小明被选中为主持人的概率；

(2)、小华和小丽被选中介绍宜昌风光，小华从四张照片中随机抽取一张，不放回；小丽再从剩下的照片中随机抽取一张.请用树状图法求小华、小丽两人中恰好有一人抽中“①号三峡大坝”的概率.

查看试题解析
20. 如图，某小区为美化生活环境，拟在一块空地上修建一个花圃，花圃形状如图所示.已知 $∠ A = ∠ D$ $= 90 °$ ， $∠ C = 120 °$ ，其中 $A D 、 D C$ 两边靠墙，另外两边由 $20$ 米长的栅栏围成.设 $B C = x$ 米，花圃的面积为y平方米.

(1)、用含有x的代数式表示出 $D C$ 的长；

(2)、求这块花圃的最大面积.

查看试题解析
21. $R t Δ A C B$ 中， $∠ A C B = 90 ° ， O$ 为 $A B$ 边上一点. $⊙ O$ 经过点 $A$ ，与 $A C ， A B$ 两边分别交于点 $E ， F$ ，连接 $E F$ .

(1)、如图1，若 $∠ B = 45 ° ， A E = 4$ ，则 $A F =$ .

(2)、如图2， $A D$ 平分 $∠ C A B$ ，交 $C B$ 于点D， $⊙ O$ 经过点D.
①求证： $B C$ 为 $⊙ O$ 的切线；

②若 $A E = 6$ ， $⊙ O$ 的半径为5，求 $C D$ 的长.

查看试题解析
22. 健康食品越来越受到人们的青睐，某公司在2016年推出 $A, B$ 两种健康食品套餐，到年底共卖出m万份，其中A套餐卖出a万份，两种套餐共获利润 $1500$ 万元、已知销售一份A套餐可获利润 $20$ 元，销售一份B套餐可获利润 $45$ 元.

(1)、用含a的代数式表示m；

(2)、随着市场需求不断变化，经营策略也随之调整.2017年，该公司将每份B套餐的利润增加到 $100$ 元，每份A套餐的利润不变.经核算，两种套餐在这一年的销售总量与2016年相同，其中A套餐的销售量增加 $\frac{1}{3}$ ，两种套餐的总利润增加 $760$ 万元.
①求2017年每种套餐的销售量；

②由于B套餐的需求量逐年上涨，而原材料供应不足，因此，2018年该公司将每份B套餐的利润在2017年的基础上增加 $x %$ ，2019年在2018年的基础上又增加 $2 x %$ 、若B套餐在近三年销售量不变的情况下，仅2019年一年就获利 $2856$ 万元，求x的值.

查看试题解析
23. 已知： $⊙ O$ 是 $Δ A B C$ 的外接圆，且 $\overset{⌢}{A B} = \overset{⌢}{B C} ， ∠ A B C = 60 ° ， D$ 为 $⊙ O$ 上一动点.
　　

(1)、如图1，若点D是 $\overset{⌢}{A B}$ 的中点，求 $∠ D B A$ 的度数.

(2)、过点B作直线 $A D$ 的垂线，垂足为点E.
①如图2，若点D在 $\overset{⌢}{A B}$ 上.求证 $C D = D E + A E$ .

②若点D在 $\overset{⌢}{A C}$ 上，当它从点A向点C运动且满足 $C D = D E + A E$ 时，求 $∠ A B D$ 的最大值.

查看试题解析
24. 如图，在平面直角坐标系中， $О$ 为坐标原点，正方形 $A B C O$ 的边 $O A$ 落在 $x$ 轴上， $O C$ 落在 $y$ 轴上， $O A = O C = 2$ ，已知直线 $l ： y = x + k$ .

(1)、填空： $B$ （，）；当直线 $l$ 与正方形 $A B C O$ 没有交点时， $k$ 的取值范围是；

(2)、当 $k = 0$ 时，已知抛物线 $L ： y = a {(x - m)}^{2} + n (a < 0 ）$ 顶点 $Р$ 在直线 $l$ 上，设抛物线与直线 $l$ 的另一个交点为 $M$ ，过 $M$ 作 $M N / / x$ 轴交抛物线于另一点 $N$ ，若 $M N = 2$ ，求 $a$ 的值；

(3)、在（2）的条件下，抛物线 $L$ 与边 $A B$ 所在的直线交于点 $E$ .
①当点 $P$ 向上运动的过程中，点 $E$ 也随之向上运动，求此时 $m$ 的取值范围，并写出点 $E$ 在最高位置时的坐标；

②若抛物线 $L$ 与线段 $O A$ 只有一个公共点，求 $m$ 的取值范围.

查看试题解析