湖南省邵阳市邵阳县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
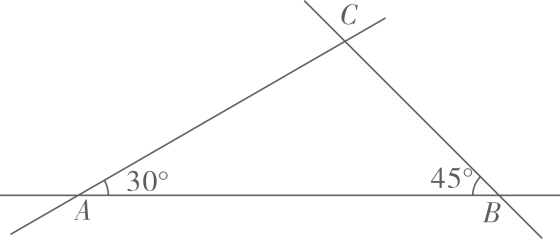
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、xy-3=52. 如果 ,那么 的值是( )A、 B、 C、 D、3. 若反比例函数 的图象在第一、第三象限,则m可能取的一个值为( )A、0 B、1 C、2 D、34. 若△ABC∽△DEF,且S△ABC:S△DEF=5:4,则△ABC与△DEF的周长比为( )A、5:4 B、4:5 C、2: D、 :25. 一元二次方程 的一般形式是( )A、 B、 C、 D、6. 已知 是线段 的黄金分割点,且 ,则 的长为( ).A、2 B、 C、2或 D、7. 如图,已知点D,E是 的三等分点, , 将 分成三部分,且 ,图中三部分的面积分别为 , , ,则 的值为( )
 A、 B、 C、 D、8. 在 中, , , ,那么下列各式中正确的是( )A、 B、 C、 D、9. 的值为( )A、1 B、2 C、 D、10. 如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )
A、 B、 C、 D、8. 在 中, , , ,那么下列各式中正确的是( )A、 B、 C、 D、9. 的值为( )A、1 B、2 C、 D、10. 如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )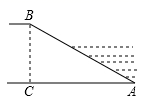 A、5m B、10m C、 m D、8m
A、5m B、10m C、 m D、8m二、填空题
-
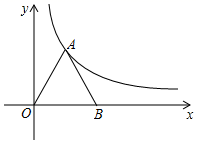
11. 在函数 的图象上有三点(﹣3,y1)、(﹣2,y2)、(1,y3),则函数值y1、y2、y3的大小关系为.12. 在平面直角坐标系中,等边 如图放置,其中 ,则过点A的反比例函数的表达式为.
 13. 若关于x的一元二次方程 的一个根是 ,则另一个根是.14. 如图,直线 ,分别交直线m,n于点A,B,C,D,E,F,若 , , ,则EF的长为.
13. 若关于x的一元二次方程 的一个根是 ,则另一个根是.14. 如图,直线 ,分别交直线m,n于点A,B,C,D,E,F,若 , , ,则EF的长为. 15. 已知 ,则 .16. 如图,在平面直角坐标系中,以原点 为位似中心,相似比为 ,将 放大为 ,已知 ,则点 的坐标为 .
15. 已知 ,则 .16. 如图,在平面直角坐标系中,以原点 为位似中心,相似比为 ,将 放大为 ,已知 ,则点 的坐标为 .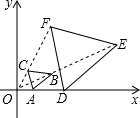 17. 已知 是锐角,且 ,那么 .18. 某斜坡坡角 的正弦值 ,则该斜坡的坡度为 .
17. 已知 是锐角,且 ,那么 .18. 某斜坡坡角 的正弦值 ,则该斜坡的坡度为 .三、解答题
-
19. 如图,点P是 的边OA上的一点,已知点P的横坐标为6,若 .
 (1)、求点P的纵坐标;(2)、求 其它的三角函数值.20. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
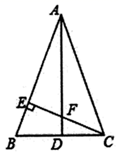
(1)、求点P的纵坐标;(2)、求 其它的三角函数值.20. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象交于点A(3,1),且过点B(0,﹣2). (1)、求反比例函数和一次函数的表达式;(2)、根据图象直接写出当 kx+b﹥ 时,x的取值范围.21. 某商场销售一批名牌衬衫,当销售价为299元时,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经试销发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫定价应多少元?22. 如图,在 中,点D在 边上, .
(1)、求反比例函数和一次函数的表达式;(2)、根据图象直接写出当 kx+b﹥ 时,x的取值范围.21. 某商场销售一批名牌衬衫,当销售价为299元时,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经试销发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫定价应多少元?22. 如图,在 中,点D在 边上, . (1)、求证: ;(2)、若 求 的长.23. 如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度, 的顶点都在格点上.
(1)、求证: ;(2)、若 求 的长.23. 如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度, 的顶点都在格点上.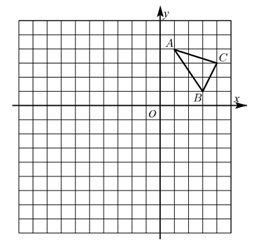 (1)、以原点O为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 .(2)、已知 的面积为 ,则 的面积是.
(1)、以原点O为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 .(2)、已知 的面积为 ,则 的面积是.