湖北省恩施土家族苗族自治州2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 方程x2=﹣x的解是( )A、x=1 B、x=0 C、x1=﹣1或x2=0 D、x1=1或x2=02. 下列图形是中心对称图形而不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 关于 的方程 有实数根,则 满足( )A、 B、 且 C、 且 D、4. 下列事件是必然事件的是( )A、抛掷一枚硬币四次,有两次正面朝上 B、打开电视频道,正在播放《在线体育》 C、射击运动员射击一次,命中十环 D、方程x2﹣2x﹣1=0必有实数根5. 对于二次函数 ,下列说法正确的是( )A、当 时, 随 的增大而增大 B、当 时, 有最大值 C、图象的顶点坐标为 D、图象与 轴有两个交点6. 如图,在 中, 是直径, 是弦, 于点M,若 ,则 的长为( )
3. 关于 的方程 有实数根,则 满足( )A、 B、 且 C、 且 D、4. 下列事件是必然事件的是( )A、抛掷一枚硬币四次,有两次正面朝上 B、打开电视频道,正在播放《在线体育》 C、射击运动员射击一次,命中十环 D、方程x2﹣2x﹣1=0必有实数根5. 对于二次函数 ,下列说法正确的是( )A、当 时, 随 的增大而增大 B、当 时, 有最大值 C、图象的顶点坐标为 D、图象与 轴有两个交点6. 如图,在 中, 是直径, 是弦, 于点M,若 ,则 的长为( ) A、 B、 C、 D、7. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率( )A、 B、 C、 D、8. 如图,在长为70 m,宽为40 m的长方形花园中,欲修宽度相等的观赏路(阴影部分所示),要使观赏路面积占总面积的 ,则路宽x应满足的方程是( )
A、 B、 C、 D、7. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率( )A、 B、 C、 D、8. 如图,在长为70 m,宽为40 m的长方形花园中,欲修宽度相等的观赏路(阴影部分所示),要使观赏路面积占总面积的 ,则路宽x应满足的方程是( ) A、(40-x)(70-x)=2450 B、(40-x)(70-x)=350 C、(40-2x)(70-3x)=2450 D、(40-2x)(70-3x)=3509. 如图,已知 ,以 为直径的圆交 于点D,过点D的 的切线交 于点E.若 ,则 的半径是( )
A、(40-x)(70-x)=2450 B、(40-x)(70-x)=350 C、(40-2x)(70-3x)=2450 D、(40-2x)(70-3x)=3509. 如图,已知 ,以 为直径的圆交 于点D,过点D的 的切线交 于点E.若 ,则 的半径是( ) A、 B、 C、 D、10. 如图,正方形 的两边 分别在x轴、y轴上,点 在边 上,以C为中心,把 旋转 ,则旋转后点D的对应点 的坐标是( ).
A、 B、 C、 D、10. 如图,正方形 的两边 分别在x轴、y轴上,点 在边 上,以C为中心,把 旋转 ,则旋转后点D的对应点 的坐标是( ). A、 B、 C、 或 D、 或11. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A、 B、 C、 或 D、 或11. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )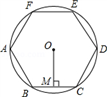 A、2, B、2 ,π C、 , D、2 ,12.
A、2, B、2 ,π C、 , D、2 ,12.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ <a<
⑤b>c.
其中含所有正确结论的选项是( )
 A、①③ B、①③④ C、②④⑤ D、①③④⑤
A、①③ B、①③④ C、②④⑤ D、①③④⑤二、填空题
-
13. 在一个不透明的盒子中装有16个白球,若干个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球是黄球的概率是 ,则黄球的个数为 .14. 某同学利用半径为40cm的扇形纸片制作成一个圆锥形纸帽(接缝忽略不计),若圆锥底面半径为10cm,那么这个圆锥的侧面积是.15.
二次函数的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
 16. 如图,在矩形 中,已知 ,矩形在直线上绕其右下角的顶点B向右旋转 至图①位置,再绕右下角的顶点继续向右旋转 至图②位置,···,以此类推,这样连续旋转 次后,顶点A在整个旋转过程中所经过的路程之和是.
16. 如图,在矩形 中,已知 ,矩形在直线上绕其右下角的顶点B向右旋转 至图①位置,再绕右下角的顶点继续向右旋转 至图②位置,···,以此类推,这样连续旋转 次后,顶点A在整个旋转过程中所经过的路程之和是.
三、解答题
-
17. 用适当的方法解方程:(1)、 ;(2)、 .18. 如图,E是正方形 中 边上一点,以点A为中心把 顺时针旋转 .
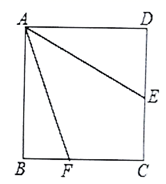 (1)、在图中画出旋转后的图形;(2)、若旋转后E点的对应点记为M,点F在 上,且 ,连接 .
(1)、在图中画出旋转后的图形;(2)、若旋转后E点的对应点记为M,点F在 上,且 ,连接 .①求证: ;
②若正方形的边长为6, ,求 .
19. 4件同型号的产品中,有1件不合格品和3件合格品.(1)、从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;(2)、从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;(3)、在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?20. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?21. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D. (1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若AC=3,∠B=30°,设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧 所围成的阴影部分的面积(结果保留根号和 ).22. 某校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第 天的售价与销量的相关信息如下表:
(1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若AC=3,∠B=30°,设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧 所围成的阴影部分的面积(结果保留根号和 ).22. 某校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第 天的售价与销量的相关信息如下表:时间x(天)
售价(元/件)
每天销量(件)
已知该商品的进价为每件 元,设销售该商品的每天利润为y元.
(1)、求y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在销售过程中,共有多少天每天销售利润不低于 元?23. 如图, 是 的直径, ,过点 作 交圆于点H,点C是弧 上异于点 的动点,过点C作 ,垂足分别为 ,过点C的直线交 的延长线于点G,且 . (1)、求证: 是O的切线;(2)、求 的长;(3)、过点C作 于点F,若 ,求 的长.24. 如图,抛物线 y=﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左边),与 y轴交于点 C,点 D 为抛物线的顶点.
(1)、求证: 是O的切线;(2)、求 的长;(3)、过点C作 于点F,若 ,求 的长.24. 如图,抛物线 y=﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左边),与 y轴交于点 C,点 D 为抛物线的顶点.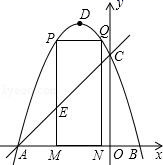 (1)、求点 A、B、C 的坐标;(2)、点 M(m,0)为线段 AB 上一点(点 M 不与点 A、B 重合),过点 M 作 x 轴的垂线,与直线 AC 交于点 E,与抛物线交于点 P,过点 P 作 PQ∥AB 交抛物线于点 Q,过点 Q 作 QN⊥x 轴于点 N,可得矩形 PQNM.如图,点 P 在点 Q 左边,试用含 m 的式子表示矩形 PQNM 的周长;(3)、当矩形 PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积;(4)、在(3)的条件下,当矩形 PMNQ 的周长最大时,连接 DQ,过抛物线上一点 F 作 y 轴的平行线,与直线 AC 交于点 G(点 G 在点 F 的上方).若 FG=2 DQ,求点 F 的坐标.
(1)、求点 A、B、C 的坐标;(2)、点 M(m,0)为线段 AB 上一点(点 M 不与点 A、B 重合),过点 M 作 x 轴的垂线,与直线 AC 交于点 E,与抛物线交于点 P,过点 P 作 PQ∥AB 交抛物线于点 Q,过点 Q 作 QN⊥x 轴于点 N,可得矩形 PQNM.如图,点 P 在点 Q 左边,试用含 m 的式子表示矩形 PQNM 的周长;(3)、当矩形 PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积;(4)、在(3)的条件下,当矩形 PMNQ 的周长最大时,连接 DQ,过抛物线上一点 F 作 y 轴的平行线,与直线 AC 交于点 G(点 G 在点 F 的上方).若 FG=2 DQ,求点 F 的坐标.