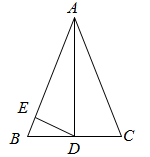广西壮族自治区贺州市八步区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 点P(-3,1)在双曲线y= 上,则k的值是( )A、-3 B、3 C、− D、2. 如图,在 中, , , , ,则 的长为( )
 A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )
A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )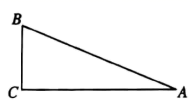 A、 B、 C、 D、4. 如图,点A在反比例函数 的图象上,过点A作 轴于点B,若 的面积为3,则k的值为( )
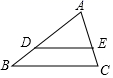
A、 B、 C、 D、4. 如图,点A在反比例函数 的图象上,过点A作 轴于点B,若 的面积为3,则k的值为( )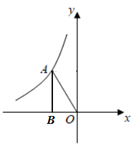 A、-6 B、6 C、-3 D、35. 抛物线y=x2﹣2x+2的顶点坐标为( )A、(1,1) B、(﹣1,1) C、(1,3) D、(﹣1,3)6. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A、-6 B、6 C、-3 D、35. 抛物线y=x2﹣2x+2的顶点坐标为( )A、(1,1) B、(﹣1,1) C、(1,3) D、(﹣1,3)6. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )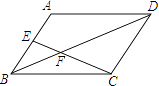 A、 B、 C、 D、7. 如图,在 中, , ,点D是 延长线上的一点,且 ,则 的值为( )
A、 B、 C、 D、7. 如图,在 中, , ,点D是 延长线上的一点,且 ,则 的值为( )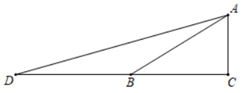 A、 B、 C、 D、8. 如图所示,在 中, ,D是 上一点, 于点E,若 , , .则 的长为( )
A、 B、 C、 D、8. 如图所示,在 中, ,D是 上一点, 于点E,若 , , .则 的长为( )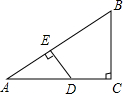 A、 B、 C、 D、9. 某广场有一个小型喷泉,水流从垂直于地面的水管 喷出, 长为 .水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为 .建立平面直角坐标系,水流喷出的高度 与水平距离 之间近似满足函数关系 ,则水流喷出的最大高度为( )
A、 B、 C、 D、9. 某广场有一个小型喷泉,水流从垂直于地面的水管 喷出, 长为 .水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为 .建立平面直角坐标系,水流喷出的高度 与水平距离 之间近似满足函数关系 ,则水流喷出的最大高度为( ) A、 B、 C、 D、10. 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE,若AB=16,BC=8,则BD的长是( )
A、 B、 C、 D、10. 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE,若AB=16,BC=8,则BD的长是( )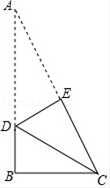 A、6 B、8 C、10 D、1211. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、6 B、8 C、10 D、1211. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、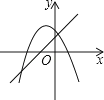 B、
B、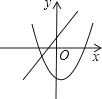 C、
C、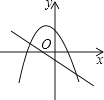 D、
D、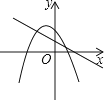 12. 如图,A、B分别是反比例函数 图象上的两点,连结 、 ,分别过点A、B作x轴的垂线,垂足分别为C、E,且 交 于点D,若 ,则 的值为( )
12. 如图,A、B分别是反比例函数 图象上的两点,连结 、 ,分别过点A、B作x轴的垂线,垂足分别为C、E,且 交 于点D,若 ,则 的值为( )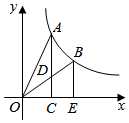 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
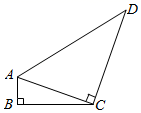
13. 抛物线y=﹣x2+5x的开口方向向(填“上”或“下”).14. 若 ,则 .15. 已知反比例函数 y= 的图象在第一、三象限,则m的取值范围是 .16. 如图所示,在四边形 中, , , .连接 , ,若 ,则 长度是.
 17. 已知二次函数 的图象如图,有下列5个结论:① ;② ;③ ;④ ;⑤ .其中正确的结论的有(填正确的序号)
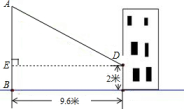
17. 已知二次函数 的图象如图,有下列5个结论:① ;② ;③ ;④ ;⑤ .其中正确的结论的有(填正确的序号)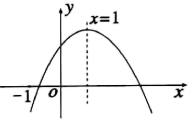 18. 赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.
18. 赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.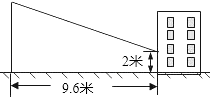
三、解答题
-
19. 计算: .20. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
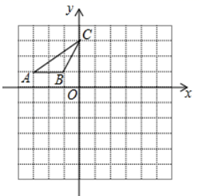
( 1 )画出 关于y轴对称的
( 2 )画出 以点O为位似中心的位似图形 , 与 的位似比为1:2;并写出 , , 的坐标
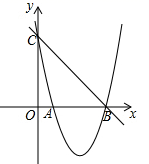
21. 如图, 是 的高, , , .求 的长.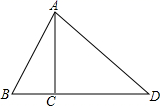 22. 已知一次函数 与反比例函数 的图象相交于点 和点 .
22. 已知一次函数 与反比例函数 的图象相交于点 和点 .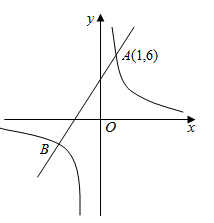 (1)、求一次函数与反比例函数的表达式;(2)、结合图象直接写出不等式 的解集.23. 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l , 是A到l的小路,现新修一条路 到公路l,小明测量出 , , .请你帮他计算出他家到公路l的距离 的长度(结果保留根号).
(1)、求一次函数与反比例函数的表达式;(2)、结合图象直接写出不等式 的解集.23. 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l , 是A到l的小路,现新修一条路 到公路l,小明测量出 , , .请你帮他计算出他家到公路l的距离 的长度(结果保留根号).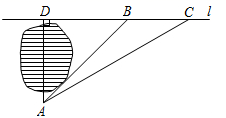 24. 某文化衫的进价为每件 元,当售价为每件 元时,每个月可售出 件.根据巿场行情,现决定涨价销售,调查反映,每涨价 元,每月要少卖出 件,设每件商品涨价x元,每个月的销量为y件.(1)、求y与x之间的函数关系式,并直接写出x的取值范围;(2)、当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?
24. 某文化衫的进价为每件 元,当售价为每件 元时,每个月可售出 件.根据巿场行情,现决定涨价销售,调查反映,每涨价 元,每月要少卖出 件,设每件商品涨价x元,每个月的销量为y件.(1)、求y与x之间的函数关系式,并直接写出x的取值范围;(2)、当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?