广西壮族自治区贵港市覃塘区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(﹣3,2)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知 是一元二次方程 的一个实根,则m的值为( )A、 B、 C、 D、3. 若反比例函数 的图象经过点 ,则该函数图象一定经过( )A、 B、 C、 D、4. 已知 为锐角,且 ,则 的度数是( )A、 B、 C、 D、5. 用配方法解一元二次方程 时,配方后得到的方程为( )A、 B、 C、 D、6. 在Rt△ABC中,若∠C=90°,BC=2AC,则cosA的值为( )A、 B、 C、 D、7. 下列说法不一定正确的是( )A、所有的等边三角形都相似 B、所有的等腰直角三角形都相似 C、所有的菱形都相似 D、所有的正方形都相似8. 关于抛物线 ,下列说法错误的是( )A、开口向上 B、与x轴有唯一交点 C、对称轴是直线 D、当 时,y随x的增大而减小9. 如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为
 A、 B、 C、 D、10. 如图,已知直线 与双曲线 相交于 和 两点,则不等式 的解集是( )
A、 B、 C、 D、10. 如图,已知直线 与双曲线 相交于 和 两点,则不等式 的解集是( ) A、 或 B、 C、 或 D、11. 如图,在 中, 是 边的中点, 于点E,交 边于点F,连接 ,则图中与 相似的三角形共有( )
A、 或 B、 C、 或 D、11. 如图,在 中, 是 边的中点, 于点E,交 边于点F,连接 ,则图中与 相似的三角形共有( ) A、2个 B、3个 C、4个 D、5个12. 如图所示是二次函数 图象的一部分,图象经过点 ,对称轴为 .给出四个结论:① ;② ;③ ;④ ,其中错误结论的序号是( )
A、2个 B、3个 C、4个 D、5个12. 如图所示是二次函数 图象的一部分,图象经过点 ,对称轴为 .给出四个结论:① ;② ;③ ;④ ,其中错误结论的序号是( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
13. 函数 的自变量x的取值范围是14. 若 是一元二次方程 的两个实数根,则 的值是.15. 二次函数 的最大值是.16. 如图,在正方形网格中,点 都是小正方形的顶点, 与 相交于点P,则 的值是.
 17. 如图,点A在双曲线 上,点B在双曲线 上,点 都在x轴上,若四边形 是矩形,且它的面积是6,则k的值是.
17. 如图,点A在双曲线 上,点B在双曲线 上,点 都在x轴上,若四边形 是矩形,且它的面积是6,则k的值是.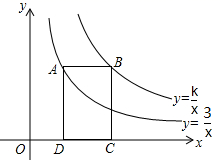 18. 如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是.
18. 如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是.
三、解答题
-
19.(1)、计算: ;(2)、解方程: .20. 如图,在平面直角坐标系中, 的顶点为 ,若 与 是以坐标原点O为位似中心的位似图形,且 的坐标为 ,请画出 ,并给出顶点 的坐标.
 21. 如图,直线 与双曲线 相交于点 将直线 向右平移m个长度单位后,与双曲线 相交于点B,与x轴相交于点C.
21. 如图,直线 与双曲线 相交于点 将直线 向右平移m个长度单位后,与双曲线 相交于点B,与x轴相交于点C. (1)、求点A的坐标(用含k的式子表示)﹔(2)、若 ,点B的横坐标为4,求双曲线的表达式.22. 某校在“校艺术节”期间,举办了A演讲、B唱歌、C书法、D绘画共四个项目的比赛.要求每位同学必须参加且限报一项.以九年级(一)班为样本进行统计,并将结果绘制如下尚不完整的条形和扇形统计图,请根据统计图解答下列问题:
(1)、求点A的坐标(用含k的式子表示)﹔(2)、若 ,点B的横坐标为4,求双曲线的表达式.22. 某校在“校艺术节”期间,举办了A演讲、B唱歌、C书法、D绘画共四个项目的比赛.要求每位同学必须参加且限报一项.以九年级(一)班为样本进行统计,并将结果绘制如下尚不完整的条形和扇形统计图,请根据统计图解答下列问题: (1)、在扇形统计图中,D项的百分率是﹔(2)、在扇形统计图中,C项的圆心角的度数是﹔(3)、请补充完整条形统计图;(4)、若该校九年级有 名学生,那么九年级参加演讲和唱歌比赛的学生共有多少人?23. 某玩具经销商2017年全年的销售总额为 万元,总成本为 万元;由于改善经营模式,与2017年相比2019年总成本下降了 销售总额增加了 .(1)、求该经销商年利润的平均增长率;(2)、如果不受客观因素的影响,并按此增长速度,那么2020年该经销商获得的利润是多少万元(结果精确到 万元).
(1)、在扇形统计图中,D项的百分率是﹔(2)、在扇形统计图中,C项的圆心角的度数是﹔(3)、请补充完整条形统计图;(4)、若该校九年级有 名学生,那么九年级参加演讲和唱歌比赛的学生共有多少人?23. 某玩具经销商2017年全年的销售总额为 万元,总成本为 万元;由于改善经营模式,与2017年相比2019年总成本下降了 销售总额增加了 .(1)、求该经销商年利润的平均增长率;(2)、如果不受客观因素的影响,并按此增长速度,那么2020年该经销商获得的利润是多少万元(结果精确到 万元).


