四川省遂宁市安居区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列选项的图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. $\sqrt{81}$ 的平方根是（）

A、 $\pm 9$ B、3 C、 $\pm 3$ D、 $- 3$

查看试题解析
3. 在实数 $\sqrt[3]{- 27}$ ，3.1415926，0.123123123…， $\frac{π}{5}$ ， $\sqrt{4}$ ， $\frac{2}{7}$ ，0.1010010001…（相邻两个1中间依次多1个0）中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下列计算正确的是（）

A、 $a^{n} \cdot a^{n} = 2 a^{n}$ B、 $c \cdot c^{5} = c^{5}$ C、 ${(3 x y^{3})}^{3} = 9 x^{3} y^{9}$ D、 $2^{6} + 2^{6} = 2^{7}$

查看试题解析
5. 已知实数x，y，m满足 $\sqrt{x + 2} + | 3x + y + m | = 0$ ，且y为负数，则m的取值范围是（）

A、m＞6 B、m＜6 C、m＞﹣6 D、m＜﹣6

查看试题解析
6. 计算 ${(- \frac{1}{3})}^{1999} \cdot {(- 3)}^{2000} =$ （）

A、 $\frac{1}{3}$ B、 $3$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
7. 若 $(x + 2) (x - 3) = x^{2} + m x - 6$ ，则 $m$ 等于（）

A、 $- 2$ B、 $2$ C、 $- 1$ D、 $1$

查看试题解析
8. 若 $x^{2} - 8 x + k$ 是完全平方式，则 $k$ 的值是（）

A、 $4$ B、 $8$ C、 $16$ D、 $32$

查看试题解析
9. 等腰三角形的周长是20cm，其中一边长4cm，则腰长为（）

A、4cm B、8cm C、4cm或8cm D、无法确定

查看试题解析
10. 下列因式分解错误的是（）

A、3x²﹣6xy＝3x（x﹣2y） B、x²﹣9y²＝（x﹣3y）（x+3y） C、4x²+4x+1＝2（x+1）² D、2x²﹣2＝2（x+1）（x﹣1）

查看试题解析
11. 国务院决定于2020年11月1日零时开展第七次全国人口普查，人口调查采用普查方式的理由是（）

A、人口调查的数目不太大 B、人口调查需要获得全面准确的信息 C、人口调查具有破坏性 D、受条件限制，无法进行抽样调查

查看试题解析
12. 如图，数轴上点A对应的数是-1，点C对应的数是-3，BC⊥AC，垂足为C，且BC=1，以A为圆心，AB长为半径画弧，交数轴于点D，则点D表示的数为（）

A、 $- 1 + \sqrt{7}$ B、 $\sqrt{2}$ C、 $- 1 + \sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
13. 角平分线的作法（尺规作图）
①以点O为圆心，任意长为半径画弧，交OA，OB于C，D两点；②分别以C，D为圆心，大于CD长为半径画弧，两弧交于点P；③过点P作射线OP，射线OP即为所求.

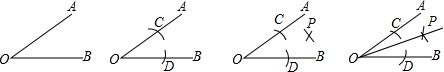
角平分线的作法依据的是（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析
14. 我市为了创建全国文明城市，经统一规划，将一正方形草坪的南北方向增加2m，东西方向缩短2m，则改造后的长方形草坪面积与原来正方形草坪面积相比（）

A、减少4m² B、增加4m² C、保持不变 D、无法确定

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ B A C$ 的平分线，若 $A C = 4$ ， $A B = 6$ ，则 $S_{△ A B D} ： S_{△ A C D} =$ （）

A、 $3 ： 2$ B、 $2 ： 3$ C、 $1 ： 1$ D、 $4 ： 3$

查看试题解析
16. 如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（）

A、 $\frac{16}{5}$ B、 $\frac{4}{5}$ C、 $\frac{8}{5}$ D、 $\frac{24}{5}$

查看试题解析
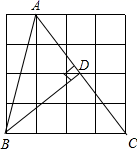17. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是（）

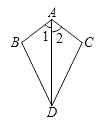A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA

查看试题解析
18. 如图：用四个全等的长方形和一个小正方形拼成如图所示的大正方形，已知大正方形的面积是 $144$ ，小正方形的面积是 $4$ ，若用 $a$ ， $b$ 分别表示矩形的长和宽（ $a > b$ ），则下列关系中不正确的是（）

A、 $a + b = 12$ B、 $a - b = 2$ C、 $a b = 35$ D、 $a^{2} + b^{2} = 84$

查看试题解析

二、填空题

19. “早发现，早报告，早隔离，早治疗”是我国抗击“新冠肺炎”的宝贵经验，其中“早”字出现的频率是.

查看试题解析
20. 因式分解：ax³y﹣axy³＝．

查看试题解析
21. $999^{2} - 998 \times 1002$ = ．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A C$ 的垂直平分线 $D E$ 分别交 $A C$ 、 $A B$ 于点 $D$ 、 $E$ ，若 $A B = 7$ ， $B C = 5$ ，则 $△ B C E$ 的周长等于.

查看试题解析
23. 计算： ${(- 3 x y)}^{3} \cdot (- x^{2} z) =$ .

查看试题解析
24. 如图，在 $△ A B C$ 中， $C P$ 平分 $∠ A C B$ ， $A P ⊥ C P$ 于点 $P$ ，已知 $△ A B C$ 的面积为 $2 c m^{2}$ ，则阴影部分的面积为 $c m^{2}$ .

查看试题解析
25. 将一根24cm的筷子，置于底面直径为5cm、高为12cm的圆柱体中，如图，设筷子露出在杯子外面长为hcm，则h的最小值， h的最大值.

查看试题解析
26. 如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：

①AD和EF互相垂直平分；

②AE=AF；

③当∠BAC=90°时，AD=EF；

④DE是AB的垂直平分线．

其中正确的是（填序号）．

查看试题解析

三、解答题

27. 计算： ${(- \sqrt{3})}^{2} + \sqrt[3]{- 8} - \sqrt{{(- 5)}^{2}} - \sqrt{\frac{1}{4}}$

查看试题解析
28. 先化简，再求值： $(3 x + 2 y) (3 x - 2 y) - 5 x (x - y) - {(2 x - y)}^{2}$ ，其中 $x = - \frac{1}{3}$ ， $y = - 2$ .

查看试题解析
29. 已知 $m^{2} + m = 2$ ，求代数式 $m^{3} + 3 m^{2} + 2020$ 的值.

查看试题解析
30. 如图，在边长为1的正方形组成的网格中， $△ A O B$ 的顶点均在格点上，点 $A$ 、 $B$ 的坐标分别是 $A (3 ， 2)$ ， $B (1 ， 3)$ ， $△ A O B$ 关于 $y$ 轴对称的图形为 $△ A_{1} O B_{1}$ .

（ 1 ）画出 $△ A_{1} O B_{1}$ ；

（ 2 ）求出 $△ A_{1} O B_{1}$ 的面积；

（ 3 ）在 $x$ 轴上找出一点P，使 $P A + P B$ 的值最小.

查看试题解析
31. 如图，等边 $△ A B C$ ，点 $P$ 在 $△ A B C$ 内，点 $Q$ 在 $△ A B C$ 外，分别连结 $A P$ 、 $B P$ 、 $A Q$ 、 $C Q$ ， $∠ A B P = ∠ A C Q$ ， $B P = C Q$ .

(1)、求证： $△ A B P ≅ △ A C Q$ ；

(2)、连结 $P Q$ ，说明 $△ A P Q$ 是等边三角形；

查看试题解析
32. 为了了解某地区初二学生课余时间活动安排情况，现对学生课余时间活动安排进行调查，根据调查的部分数据绘制成如图所示的扇形统计图和条形统计图（均不完整），请根据图中所给信息解答下列问题：

(1)、求调查中，一共抽查了多少名初二同学？

(2)、求所调查的初二学生课余时间用于安排“读书”活动人数，并补全条形统计图；

(3)、如果该地区现有初二学生12000人，那么利用课余时间参加“体育”锻炼活动的大约有多少人？

查看试题解析
33. 如图，在长方形 $A B C D$ 中， $A B = C D = 6 c m$ ， $B C = 10 c m$ ，点 $P$ 从点 $B$ 出发，以 $2 c m$ /秒的速度沿 $B C$ 向点 $C$ 运动，设点 $P$ 的运动时间为 $t$ 秒：

(1)、 $P C =$ $c m$ .（用 $t$ 的代数式表示）

(2)、当 $t$ 为何值时， $△ A B P ≅ △ D C P$ ？

(3)、当点 $P$ 从点 $B$ 开始运动，同时，点 $Q$ 从点 $C$ 出发，以 $v$ $c m$ /秒的速度沿 $C D$ 向点 $D$ 运动，是否存在这样 $v$ 的值，使得 $△ A B P$ 与 $△ P Q C$ 全等？若存在，请求出 $v$ 的值；若不存在，请说明理由.

查看试题解析