四川省绵阳市名校联盟2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若关于 $x$ 的代数式 $x^{0} + a$ 在实数范围内有意义，则（）

A、 $x = 0$ B、 $a = 0$ C、 $a \neq 0$ D、 $x \neq 0$

查看试题解析
2. 下面四个图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若三角形的两边长分别为 $2$ ， $6$ ，则此三角形第三边的长可能是（）

A、 $3$ B、 $4$ C、 $5$ D、 $9$

查看试题解析
4. 如图，在 $△ A B C$ 中， $A D$ ， $A E$ 分别是边 $B C$ 上的中线与高， $A E = 8$ ， $△ A B C$ 的面积为 $24$ ，则 $C D$ 的长为（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
5. 据悉，华为Mate40 Pro和华为Mate40 Pro+搭载业界首款 $5 n m$ 麒麟 $9000 5 GSoC$ 芯片，其中 $5 n m$ 就是 $0.000000005 m$ .将数据 $0.000000005$ 用科学记数法表示为（）

A、 $5 \times 10^{- 9}$ B、 $0.5 \times 10^{- 8}$ C、 $5 \times 10^{- 7}$ D、 $5 \times 10^{7}$

查看试题解析
6. 如图，点B，E，C，F在一条直线上， $△ A B C ≅ △ D F E$ ，则下列结论正确的是（）

A、 $∠ A B E = ∠ G E C$ B、 $A B = D E$ C、 $∠ A C B = ∠ D F E$ D、 $A G = D G$

查看试题解析
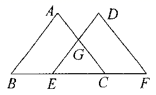7. 如图，正六边形螺帽，点 $A$ ， $B$ ， $C$ 为它的三个顶点，则 $∠ A B C =$ （）

A、 $15 °$ B、 $28 °$ C、 $29 °$ D、 $30 °$

查看试题解析
8. 若计算关于 $x$ 的代数式 $(1 - x) (x^{2} + m x + 2)$ 得 $x^{2}$ 的系数为 $3$ ，则 $m =$ （）

A、 $- 4$ B、 $- 2$ C、 $2$ D、 $4$

查看试题解析
9. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批椽，这批椽的价钱为 $6210$ 文.如果每株椽的运费是 $3$ 文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问 $6210$ 文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x + 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $3 x = \frac{6210}{x + 1}$

查看试题解析
10. 如图，四边形 $A B C D$ 中， $∠ A = ∠ B = 90 °$ ， $∠ C = 60 °$ ， $C D = 2 A D$ ， $A B = 4$ ，点 $P$ 是 $A B$ 上一动点，则 $P C + P D$ 的最小值是（）

A、 $4$ B、 $6$ C、 $8$ D、 $10$

查看试题解析
11. 若 $2^{m} = 3$ ， $3 \times 2^{n - m} = 2$ ，则 $m^{0} + {(- 2021)}^{n} =$ （）

A、 $2021$ B、 $- 2020$ C、 $- 2021$ D、 $- 2022$

查看试题解析
12. 如图，在长方形 $A B C D$ 中， $A F ⊥ B D$ ，垂足为 $E$ ， $A F$ 交 $B C$ 于点 $F$ ，连接 $D F$ ，且 $D F$ 平分 $∠ B D C$ .下列结论中：① $△ A B D ≅ △ C D B$ ；② $S_{△ A D E} = S_{△ B D F}$ ；③ $∠ A B D + ∠ C D F = 90 °$ ；④ $A D = D F$ .其中正确的个数有（）

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析

二、填空题

13. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
14. 在平面直角坐标系中，点 $A (a, \sqrt{3})$ 与点 $B (2, b)$ 关于 $x$ 轴对称，则 $b^{- a} =$ .

查看试题解析
15. 如图， $△ A B C$ 是正三角形，点 $D$ 为三边中线的交点，则 $∠ A D B =$ 度.

查看试题解析
16. 如图，把一张长方形的纸沿对角线折叠，若 $∠ A B C = 118 °$ ，则 $∠ B A C =$ .

查看试题解析
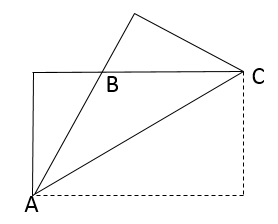17. 如图，一块直径为 $a + b$ 的圆形彩色纸板，从中挖去直径分别为 $a$ 与 $b$ 的两个小圆，若 $a - b = 3$ ， $a^{2} + b^{2} = 19$ ，则剩下的纸板的面积是.

查看试题解析
18. 有一个三角形纸片 $A B C$ ， $∠ A = 76 °$ ，点 $D$ 是 $A C$ 边上一点，沿 $B D$ 方向剪开三角形纸片后，发现所得两个纸片均为等腰三角形，则 $∠ C =$ .

查看试题解析

三、解答题

19.

(1)、因式分解： $m n^{3} - 4 m^{3} n$ ；

(2)、先化简，再求值： $[x (x^{- 2} y^{2} - x y) + x^{2} y + \frac{1}{2} x {(x^{- 1} y)}^{2}] \div 3 x^{- 2} y$ ，其中 $x$ 与 $y$ 互为倒数.

查看试题解析
20. 计算： $1 \div (2 x - \frac{1 + x^{2}}{x}) - \frac{x - 1}{x^{2} - 2 x + 1}$ .

查看试题解析
21. 如图， $A B = D B$ ， $∠ A B D = ∠ A C D$ ， $A C$ 与 $B D$ 交于点 $F$ ，点 $E$ 在线段 $A F$ 上， $A E = D C$ ， $∠ D B E = 6 °$ ， $∠ B C D = 108 °$ .

(1)、求证： $△ B C D ≅ △ B E A$ ；

(2)、求 $∠ A F D$ 的度数.

查看试题解析
22. 清江山水华府小区物业，将对小区内部非活动区域进行绿化.甲工程队用 $m$ 天完成这项工程的三分之一，为加快工程进度，乙工程队参与绿化建设，两队合作用 $5$ 天完成这一项工程.

(1)、若 $m = 10$ ，求乙工程队单独完成这项工程所需的时间；

(2)、求 $m$ 的取值范围.

查看试题解析
23. 如图，在多边形 $A B C D E$ 中， $B C ⊥ C D$ ， $B F ⊥ A E$ 于点 $F$ ，且 $B F = B C$ ， $∠ C B F = 2 ∠ D B E$ ， $∠ A B F = ∠ C B D$ .

(1)、求证： $A B = D B$ ；

(2)、若 $D E = 4$ ， $B F = 3$ ，求 $△ B D E$ 的面积.

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，点 $A$ 在 $x$ 轴上，点 $B$ 在第一象限， $∠ O A C = 38 °$ ， $∠ A C O = 22 °$ ， $O C$ 平分 $∠ B O D$ ， $A C = B C$ ，点 $A$ ， $B$ 的横坐标分别为 $x_{A}$ ， $x_{B}$ ，且 $0 < x_{A} < x_{B}$ .

(1)、求 $∠ A O B$ 的度数；

(2)、求证： $∠ C A O = ∠ O B C$ ；

(3)、设点 $C$ 的横坐标为 $x_{C}$ ，求证： $x_{A} = 2 (x_{B} + x_{C})$ .

查看试题解析