陕西省咸阳市秦都区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{a}$ 不是无理数，则a可以取的值是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 下列选项中，可以用来说明命题“若x²＞9，则x＞3”是假命题的反例是（）

A、 $x = 6$ B、 $x = 5$ C、 $x = 4$ D、 $x = - 4$

查看试题解析
3. 下列各组数中，以 $a$ ， $b$ ， $c$ 为边的三角形不是直角三角形的是（）

A、 $a = 7$ ， $b = 25$ ， $c = 24$ B、 $a = 3$ ， $b = 3$ ， $c = 4$ C、 $a = 6$ ， $b = 8$ ， $c = 10$ D、 $a = 8$ ， $b = 17$ ， $c = 15$

查看试题解析
4. 已知正比例函数 $y = k x (k \neq 0)$ ，且 $y$ 随 $x$ 的增大而减小，则该函数的图象经过（）

A、第二、四象限 B、第一、三象限 C、第一、二象限 D、第二、三象限

查看试题解析
5. 如图，直线 $a ， b$ 与直线 $c ， d$ 相交，已知 $∠ 1 = ∠ 2 ，$ $∠ 3 = 100 °$ ，则 $∠ 4$ 的度数是（）

A、 $70^{\circ}$ B、 $80^{\circ}$ C、 $110^{\circ}$ D、 $100^{\circ}$

查看试题解析
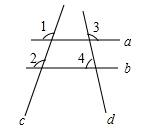6. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85、90、95，则该选手的综合成绩为（）

A、92 B、88 C、90 D、95

查看试题解析
7. 若实数 $k$ 、 $b$ 满足 $k + b = 0$ ，且 $k > b$ ，则一次函数 $y = k x + b$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，10块相同的小长方形墙砖拼成一个大长方形，设小长方形墙砖的长为 $x$ 厘米，宽为 $y$ 厘米，则依题意列二元一次方程组正确的是（）

A、 ${\begin{array}{l} 5 x + 2 y = 75 \\ y = 3 x \end{array}$ B、 ${\begin{array}{l} 2 x + y = 75 \\ y = 3 x \end{array}$ C、 ${\begin{array}{l} x + 2 y = 75 \\ x = 3 y \end{array}$ D、 ${\begin{array}{l} 2 x + y = 75 \\ x = 3 y \end{array}$

查看试题解析
9. 如图，在△ABC中，点E和F分别是AC，BC上一点，EF∥AB，∠BCA的平分线交AB于点D，∠MAC是△ABC的外角，若∠MAC＝α，∠EFC＝β，∠ADC＝γ，则α、β、γ三者间的数量关系是（）

A、β＝α+γ B、β＝2γ﹣α C、β＝α+2γ D、β＝2α﹣2γ

查看试题解析
10. 某乡村盛产葡萄，果大味美，甲、乙两个葡萄采摘园为吸引游客，在销售价格一样的基础上分别推出优惠方案，甲采摘园的优惠方案：游客进园需购买门票，采摘的所有葡萄按六折优惠．乙采摘园的优惠方案：游客无需买票，采摘葡萄超过一定数量后，超过的部分打折销售．活动期间，某游客的葡萄采摘量为xkg，若在甲采摘园所需总费用为y_甲元，若在乙采摘园所需总费用为y_乙元，y_甲、y_乙与x之间的函数图象如图所示，则下列说法错误的是（）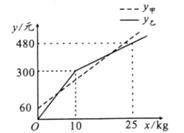

A、甲采摘园的门票费用是60元 B、两个采摘园优惠前的葡萄价格是30元/千克 C、乙采摘园超过10kg后，超过的部分价格是12元/千克 D、若游客采摘18kg葡萄，那么到甲或乙两个采摘园的总费用相同

查看试题解析

二、填空题

11. 小于 $\sqrt{17}$ 的最大整数是

查看试题解析
12. 如图，在同一直角坐标系中作出一次函数 $y = k_{1} x$ 与 $y = k_{2} x + b$ 的图象，则关于 $x$ 、 $y$ 的二元一次方程组 ${\begin{array}{l} y = k_{1} x \\ y = k_{2} x + b \end{array}$ 的解是.

查看试题解析
13. 如图， $∠ A B C + ∠ C + ∠ C D E = 360 °$ ，直线 $F G$ 分别交AB、DE于点F、G.若 $∠ 1 = 110 °$ ，则 $∠ 2 =$ .

查看试题解析
14. 如图，长方体的棱AB长为4，棱BC长为3，棱BF长为2，P为HG的中点，一只蚂蚁从点A出发，沿长方体的表面爬行到点 $P$ 处吃食物，那么它爬行的最短路程是.

查看试题解析

三、解答题

15. 计算： $\sqrt{48} \times \sqrt{\frac{1}{3}} - \sqrt{8} \div \sqrt{2} - {(\sqrt{2})}^{2}$ .

查看试题解析
16. 解方程组 ${\begin{matrix} 3x+2y=12 \\ 3x-y=3 \end{matrix}$

查看试题解析
17. 已知某正数的两个平方根是 $3 a - 14$ 和 $a + 2$ ， $b - 14$ 的立方根为－2，求 $a + b$ 的算术平方根.

查看试题解析
18. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点都在格点上，且 $A (2 ， 4)$ ， $A (2 ， 4)$ ， $C (5 ， 3)$ .

(1)、画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；

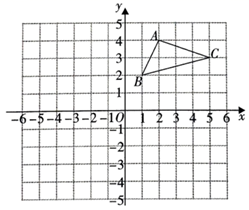(2)、在（1）的条件下，分别写出点A、C的对应点 $A_{1}$ 、 $C_{1}$ 的坐标.

查看试题解析
19. 如图，AD是△ABC的中线，AD＝12，AB＝13，BC＝10，求AC长.

查看试题解析
20. 如图，在 $△ A B C$ 中，∠B=25°，∠BAC=31°，过点A作BC边上的高，交BC的延长线于点D ， CE平分∠ACD ，交AD于点E ．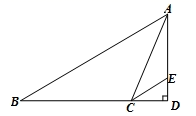
求：

(1)、∠ACD的度数；

(2)、∠AEC的度数．

查看试题解析
21. 如图，直线 $l$ 是一次函数 $y = k x + b$ 的图象.

(1)、求出这个一次函数的解析式；

(2)、将该函数的图象向下平移3个单位，求出平移后一次函数的解析式，并写出平移后的图象与 $x$ 轴的交点坐标

查看试题解析
22. 如图，已知点E在直线DC上，射线EF平分 $∠ A E D$ ，过E点作 $E B ⊥ E F$ ，G为射线EC上一点，连接BG，且 $∠ E B G + ∠ B E G = 90 °$ .

(1)、求证： $∠ D E F = ∠ E B G$ ；

(2)、若 $∠ E B G = ∠ A$ ，求证： $A B // E F$ .

查看试题解析
23. 在一次广场舞比赛中，甲、乙两个队参加表演的女演员的身高（单位：cm）分别是甲队：163 165 165 164 168
乙队：162 164 164 167 168

(1)、求甲队女演员身高的平均数、中位数﹑众数；

(2)、计算两队女演员身高的方差，并判断哪个队女演员的身高更整齐？

查看试题解析

24. 某电器超市销售每台进价为80元、200元的A，B两种型号的电风扇，如表所示是六月份前2周的销售情况：(进价、售价均保持不变，利润=销售收入﹣进货成本)

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	6	5	2100元
第二周	4	10	3400元

(1)、求A、B两种型号的电风扇的销售单价.

(2)、若超市一共采购这两种型号的电风扇共120台，售完后该超市能否实现利润为8000元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

25. 某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表

$x$ （单位：台）

10

20

$y$ （单位：万元/台）

60

55

(1)、求y与x之间的函数关系式；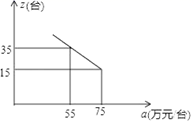

(2)、市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润.（注：利润＝售价﹣成本）

查看试题解析

$x$ （单位：台）	10	20
$y$ （单位：万元/台）	60	55