陕西省西安市雁塔区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 3的立方根是（）

A、 1 B、 $\sqrt{3}$ C、 $\sqrt[3]{3}$ D、 $- \sqrt[3]{3}$

查看试题解析
2. 已知小红从点O出发，先向西走20米，再向北走10米，到达点C，如果点C的位置用 $(- 20 ， 10)$ 表示，那么用 $(10 ， - 10)$ 表示的位置的点是（）

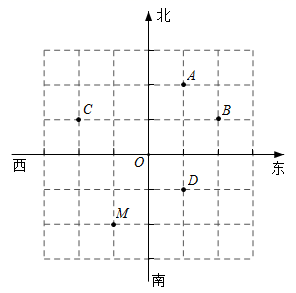A、点A B、点B C、点C D、点D

查看试题解析
3. 下列命题中，真命题是（）

A、如果 $a^{2} = b^{2}$ ，那么 $a = b$ B、如果两个角相等，那么它们是对顶角 C、两直线平行，同旁内角互补 D、三角形的一个外角大于任何一个内角

查看试题解析
4. 下列四组线段中，不能组成直角三角形的是（）

A、 $a = 5$ ， $b = 12$ ， $c = 13$ B、 $a = 6$ ， $b = 8$ ， $c = 10$ C、 $a = 7$ ， $b = 24$ ， $c = 25$ D、 $a = 8$ ， $b = 12$ ， $c = 15$

查看试题解析
5. 如图，已知直线 $A B // C D$ ， $∠ A = 25 °$ ， $∠ E = 90 °$ ，则 $∠ C$ 的度数为（）

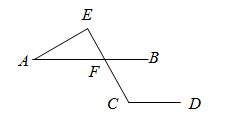A、115° B、95° C、90° D、65°

查看试题解析
6. 在式子 $y = (m - 1) x + n$ 中，若y是x的正比例函数，则m，n应满足的条件是（）

A、 $m \neq 1$ B、 $m \neq 1$ ，且 $n = 0$ C、 $m = 1$ ，且 $n = 0$ D、 $n = 0$

查看试题解析
7. 在抗击新型冠状病毒肺炎疫情中，某社区志愿者小分队10名队员年龄统计如下表：

年龄（岁）

18

22

30

35

43

人数

2

3

2

2

1

则这10名队员年龄的中位数、众数分别是（）

A、20岁，35岁 B、26岁，22岁 C、22岁，26岁 D、30岁，30岁

查看试题解析
8. 《九章算术》中有一道“盈不足术”问题，原文为：今有人共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文为：现有一些人共同购买一个物品，每人出8元，还盈余3元；每人出7元，还差4元，问共有多少人？这个物品的价格是多少？设共同购买物品的有x人，该物品的价格为y元，则根据题意，列出的方程组为（）

A、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = - 4 \end{array}$ B、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ C、 ${\begin{array}{l} 8 y - x = 3 \\ 7 y - x = 4 \end{array}$ D、 ${\begin{array}{l} 8 y - x = - 3 \\ 7 y - x = - 4 \end{array}$

查看试题解析

二、填空题

9. 计算： $\frac{\sqrt{6} \times \sqrt{8}}{\sqrt{2}} =$ .

查看试题解析
10. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是二元一次方程 $2 x - a y = 5$ 的一个解，则a的值为.

查看试题解析
11. 如图， $△ A B C$ 中， $A D$ 是高， $A E$ 是 $∠ B A C$ 的平分线， $∠ B = 70 °$ ， $∠ D A E = 19 °$ ，则 $∠ C$ 的度数是.

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，将四边形 $A B C D$ 先向下平移，再向右平移，得到四边形 $A_{1} B_{1} C_{1} D_{1}$ ，已知点 $A (- 3 ， 5)$ ，点 $B (- 4 ， 3)$ ，点 $A_{1} (3 ， 3)$ ，则点 $B_{1}$ 的坐标为.

查看试题解析
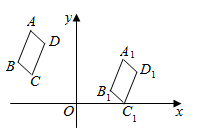13. 如图是一棵勾股树，它是由正方形和直角三角形排成的，若正方形A，B，C，D的边长分别是4，5，3，4，则最大正方形E的面积是.

查看试题解析
14. 如图，直线 $l_{1}$ ， $l_{2}$ 的交点坐标可以看做方程组的解.

查看试题解析

三、解答题

15. 如图在平面直角坐标系中， $△ A B C$ 顶点的坐标分别为：A(4，0)，B(-1，4)，C(-3，1)

(1)、在图中作 $△ A^{'} B^{'} C^{'}$ 使 $△ A^{'} B^{'} C^{'}$ 和 $△ A B C$ 关于x轴对称；

(2)、写出点 $A^{'} 、 B^{'} 、 C^{'}$ 的坐标.

查看试题解析
16. 计算：

(1)、 $\sqrt{7} - \sqrt{\frac{1}{7}}$ ；

(2)、 $(\sqrt{5} + 3) (\sqrt{5} - 2)$ .

查看试题解析
17. 解方程组：

(1)、 ${\begin{array}{l} 4 x - y = 5 \\ y = 2 x - 1 \end{array}$

(2)、 ${\begin{array}{l} 2 x - y = 2 \\ 4 x + 3 y = - 7 \end{array}$

查看试题解析
18. 如图， $∠ 1 = 78 °$ ， $∠ 2 = 102 °$ ， $∠ C = ∠ D$ .求证： $A C // D F$ .

查看试题解析

19. 甲、乙两台机床同时生产一种零件，在10天中，两台机床每天出次品的数量如表：

甲（件）	3	1	2	2	2	0	3	1	2	4
乙（件）	2	3	3	1	3	2	2	1	2	1

(1)、计算甲、乙两台机床每天出次品的平均数；

(2)、若出次品的波动性比较小的机床为性能较好的机床，试判断哪台机床的性能更好，并说明理由.

查看试题解析

20. 小颖家离学校 $1880 m$ ，其中有一段为上坡路，另一段为下坡路，她跑步去学校共用了 $16 min$ ，已知小颖在上坡路上的平均速度是 $4 .8km/h$ ，在下坡路上的平均速度是 $12 km/h$ .小颍上坡、下坡各用了多长时间？

查看试题解析
21. 已知一次函数 $y = k x + b$ ，当 $x = 1$ 时， $y = - 1$ ；当 $x = - 1$ ， $y = - 5$ .

(1)、在所给坐标系中画出一次函数 $y = k x + b$ 的图象：

(2)、求k，b的值；

(3)、将一次函数 $y = k x + b$ 的图象向上平移2个单位长度，求所得到新的函数图象与x轴、y轴的交点坐标.

查看试题解析
22. 如图（1）所示，在A，B两地间有一车站C，一辆汽车从A地出发经C站匀速驶往B地 $.$ 如图（2）是汽车行驶时离C站的路程 $y ($ 千米 $)$ 与行驶时间 $x ($ 小时 $)$ 之间的函数关系的图象.

(1)、填空： $a =$ km，AB两地的距离为km；

(2)、求线段PM、MN所表示的y与x之间的函数表达式；

(3)、求行驶时间x在什么范围时，小汽车离车站C的路程不超过60千米？

查看试题解析

年龄（岁）	18	22	30	35	43
人数	2	3	2	2	1