江苏省泰州市兴化市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列交通指示标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,适合用普查的是( )A、夏季冷饮市场上冰淇淋的质量 B、某本书上的印刷错误 C、公民保护环境的意识 D、长江中现有鱼的种类3. 下列各点中,位于第二象限的是( )A、 B、 C、 D、4. 在 中, ,如果 ,那么 的度数为( )A、40° B、70° C、100° D、40°或70°5. 在满足下列条件的 中,不是直角三角形的是( )A、 B、 C、 D、6. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则不等式 的解集为( )
2. 下列调查中,适合用普查的是( )A、夏季冷饮市场上冰淇淋的质量 B、某本书上的印刷错误 C、公民保护环境的意识 D、长江中现有鱼的种类3. 下列各点中,位于第二象限的是( )A、 B、 C、 D、4. 在 中, ,如果 ,那么 的度数为( )A、40° B、70° C、100° D、40°或70°5. 在满足下列条件的 中,不是直角三角形的是( )A、 B、 C、 D、6. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则不等式 的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 9的算术平方根是 .8. 数149000000用科学记数法表示可记为 .9. 如图,在Rt△ABC中,∠ACB=90°,D 为 AB 中点,CD=2,则AB= .
 10. 如图, , , ,则 .
10. 如图, , , ,则 .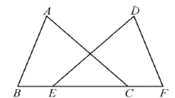 11. “小明家买彩票将获得500万元大奖”是事件.(填“必然”、“不可能”或“随机”)12. 平面直角坐标系中,若点 在 轴上,则 的值为 .13. 已知点 在一次函数 的图像上,则 的值是 .14. 将函数 的图象向上平移3个单位长度,得到的函数图象的解析式为.15. 如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面的部分 为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部 恰好碰到岸边的 ,则这根芦苇的长度是尺.
11. “小明家买彩票将获得500万元大奖”是事件.(填“必然”、“不可能”或“随机”)12. 平面直角坐标系中,若点 在 轴上,则 的值为 .13. 已知点 在一次函数 的图像上,则 的值是 .14. 将函数 的图象向上平移3个单位长度,得到的函数图象的解析式为.15. 如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面的部分 为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部 恰好碰到岸边的 ,则这根芦苇的长度是尺. 16. 已知正比例函数 的图像经过点 ,点 在正比例函数 的图像上,点 ,且 ,则点 的坐标为 .
16. 已知正比例函数 的图像经过点 ,点 在正比例函数 的图像上,点 ,且 ,则点 的坐标为 .三、解答题
-
17. 计算与求值(1)、计算: ;(2)、求 中 的值.18. 已知 与 成正比例,且当 时, .(1)、求出 与 之间的函数关系式;(2)、点 、 都在(1)中的函数图象上,判定 和 的大小关系,并说明理由.19. 如图, 中, , , .
 (1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.20. 光明中学为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
(1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.20. 光明中学为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)、在这次调查中,该学校一共抽样调查了名学生;(2)、在扇形统计图中“骑车”一项对应的扇形圆心角的度数是°;(3)、补全条形统计图;(4)、若该学校共有1800名学生,试估计该学校学生中选择“步行”方式的人数.21. 如图,在 中, , , ,垂足为 、 , 、 相交于点 .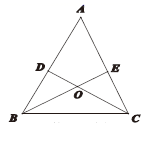 (1)、求证: ;(2)、求证: .22. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 、 、 .
(1)、求证: ;(2)、求证: .22. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 、 、 .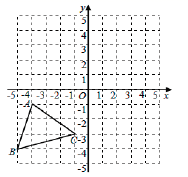 (1)、写出点 关于 轴的对称点 的坐标;(2)、请在图中画出 关于 轴对称的 ;(3)、写出 的面积, ;(4)、在 轴上找点 ,使 的值最小,在图中画出点 .23. 如图, 中, 的垂直平分线分别交 、 于点 、 , 的垂直平分线分别交 、 于点 、 , 的周长是7.
(1)、写出点 关于 轴的对称点 的坐标;(2)、请在图中画出 关于 轴对称的 ;(3)、写出 的面积, ;(4)、在 轴上找点 ,使 的值最小,在图中画出点 .23. 如图, 中, 的垂直平分线分别交 、 于点 、 , 的垂直平分线分别交 、 于点 、 , 的周长是7. (1)、求 的长度;(2)、若 ,则 度数是多少?请说明理由.24. 供销商场购进甲、乙两种洗衣机共80台进行销售,其中乙洗衣机的数量不超过甲洗衣机的3倍,甲洗衣机每台利润为500元,乙洗衣机每台利润为600元.设购进甲洗衣机 (台),这80台洗衣机全部售出的总利润为 (元).(1)、求 关于 的函数表达式;(2)、当甲洗衣机购进多少台时,销售总利润最大?最大利润是多少?25. 已知:如图, 中, , ,点 是 的中点,点 是直线 上的一个动点,连接 ,过点 作 交直线 于点 .
(1)、求 的长度;(2)、若 ,则 度数是多少?请说明理由.24. 供销商场购进甲、乙两种洗衣机共80台进行销售,其中乙洗衣机的数量不超过甲洗衣机的3倍,甲洗衣机每台利润为500元,乙洗衣机每台利润为600元.设购进甲洗衣机 (台),这80台洗衣机全部售出的总利润为 (元).(1)、求 关于 的函数表达式;(2)、当甲洗衣机购进多少台时,销售总利润最大?最大利润是多少?25. 已知:如图, 中, , ,点 是 的中点,点 是直线 上的一个动点,连接 ,过点 作 交直线 于点 . (1)、如图,当点 、 分别在线段 、 上时(点 与点 、 不重合),过点 作 的平行线交 的延长线于点 ,连接 、 .
(1)、如图,当点 、 分别在线段 、 上时(点 与点 、 不重合),过点 作 的平行线交 的延长线于点 ,连接 、 .①求证: ;
②若 , ,设 , ,求 关于 的函数表达式.
(2)、当点 在线段 的延长线上时,依据题意补全下图,用等式表示线段 、 、 之间的数量关系,并说明理由. 26. 已知:直线 和 .(1)、当 时,若 ,求 的取值范围;(2)、当 时, ,直接写出 的取值范围.(3)、若直线 经过点 ,
26. 已知:直线 和 .(1)、当 时,若 ,求 的取值范围;(2)、当 时, ,直接写出 的取值范围.(3)、若直线 经过点 ,①求 的函数表达式及直线 与 的交点坐标;
②已知直线 与 、 、 轴分别有三个不同交点 、 、 ,当点 、 、 中的一个点到另外两个点的距离相等时,求 的值.
