江苏省连云港市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列各式中,正确的是( )A、 B、 C、 D、2. 从2019年末到2020年5月2日截止,世界各国感染新冠状肺炎病毒患者达到3315003人,将数据3315003四舍五入精确到万位,用科学记数法表示为( )A、332×104 B、3.31×106 C、3.32×106 D、3.315×1063. 若点P(x, y)在第二象限,且 ,则x + y =( )A、-1 B、1 C、5 D、-54. 若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知一次函数 ,函数值 随自变量 的增大而减小,那么 m 的取值范围是( )A、 B、 C、 D、6. 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
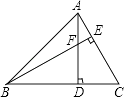 A、 B、4 C、 D、7. 如图,在 中, , , 为 的平分线,将 沿直线 翻折得 ,则 的长为( )
A、 B、4 C、 D、7. 如图,在 中, , , 为 的平分线,将 沿直线 翻折得 ,则 的长为( ) A、4 B、5 C、6 D、78. 火车匀速通过隧道时,火车在隧道内的长度 (米)与火车行驶时间 (秒)之间的关系用图像描述如图所示,有下列结论:①火车的速度为30米/秒;②火车的长度为120米;③火车整体都在隧道内的时间为35秒;④隧道长度为1200米.其中正确的结论是( )
A、4 B、5 C、6 D、78. 火车匀速通过隧道时,火车在隧道内的长度 (米)与火车行驶时间 (秒)之间的关系用图像描述如图所示,有下列结论:①火车的速度为30米/秒;②火车的长度为120米;③火车整体都在隧道内的时间为35秒;④隧道长度为1200米.其中正确的结论是( ) A、①②③ B、①②④ C、③④ D、①③④
A、①②③ B、①②④ C、③④ D、①③④二、填空题
-
9. 的算术平方根是10. 已知点M(x,3)与点N(-2,y)关于x轴对称,则3x+2y= .11. 在实数 ,0, , , ,0.20202中,无理数有个.12. 已知实数 , 满足 ,则以 , 的值为两边长的等腰三角形的周长是 .13. 如图,点 是等边 内的一点, , , .若点 是 外的一点,且 ,则 的度数为 .
 14. 如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组 的解为。
14. 如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组 的解为。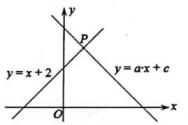 15. 如图,已知点 ,直线 与两坐标轴分别交于A , B两点,D , E分别是AB , OB上的动点,则 周长的最小值是 .
15. 如图,已知点 ,直线 与两坐标轴分别交于A , B两点,D , E分别是AB , OB上的动点,则 周长的最小值是 . 16. 如图,正方形 的边长为2, 为坐标原点, 和 分别在 轴、 轴上,点 是 边的中点,过点 的直线 交线段 于点 ,连接 ,若 平分 ,则 的值为 .
16. 如图,正方形 的边长为2, 为坐标原点, 和 分别在 轴、 轴上,点 是 边的中点,过点 的直线 交线段 于点 ,连接 ,若 平分 ,则 的值为 .
三、解答题
-
17. 计算: .18. 求下列各式中的 :(1)、 ;(2)、 .19. 已知 与 成正比例且 时, .(1)、求 与 之间的函数关系式;(2)、若点 在这个函数的图象上,求 的值.20. 课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
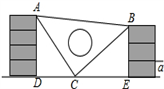 (1)、求证:△ADC≌△CEB;(2)、从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).21. 如图,一只蚂蚁从点 沿数轴向右爬了2个单位长度到达点 ,点 表示 ,设点 所表示的数为 .
(1)、求证:△ADC≌△CEB;(2)、从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).21. 如图,一只蚂蚁从点 沿数轴向右爬了2个单位长度到达点 ,点 表示 ,设点 所表示的数为 .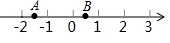 (1)、求 的值;(2)、在数轴上还有 、 两点分别表示实数 和 ,且有 与 互为相反数,求 的平方根.22. 为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1000米2的面积进行消杀.(1)、设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;(2)、在现有资金不超过5300元的情况下,求可消杀的最大面积.23. 如图,在等边 中, 是 的角平分线, 为 上一点,以 为一边且在 下方作等边 ,连接 .
(1)、求 的值;(2)、在数轴上还有 、 两点分别表示实数 和 ,且有 与 互为相反数,求 的平方根.22. 为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1000米2的面积进行消杀.(1)、设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;(2)、在现有资金不超过5300元的情况下,求可消杀的最大面积.23. 如图,在等边 中, 是 的角平分线, 为 上一点,以 为一边且在 下方作等边 ,连接 . (1)、求证: ;(2)、延长 至 , 为 上一点,连接 、 使 ,若 时,求 的长.24. 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a(a 0).
(1)、求证: ;(2)、延长 至 , 为 上一点,连接 、 使 ,若 时,求 的长.24. 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a(a 0). (1)、当a=1时,求直线BC的解析式;(2)、在(1)的条件下,请直接写出k1x+b1 k2x+b2时,对应的x的取值范围;(3)、设△ABC的面积为S,用含a的代数式表示S,并求出当直线CB把△ACD的面积分为1:2的两部分时,对应a的值.25. 甲、乙两车分别从相距480千米的 、 两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经 地,甲车到达 地停留1小时,因有事按原路原速返回 地.乙车从 地直达 地,两车同时到达 地.甲、乙两车距各自出发地的路程 (千米)与甲车出发后所用的时间 (时)的函数图象如图所示.
(1)、当a=1时,求直线BC的解析式;(2)、在(1)的条件下,请直接写出k1x+b1 k2x+b2时,对应的x的取值范围;(3)、设△ABC的面积为S,用含a的代数式表示S,并求出当直线CB把△ACD的面积分为1:2的两部分时,对应a的值.25. 甲、乙两车分别从相距480千米的 、 两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经 地,甲车到达 地停留1小时,因有事按原路原速返回 地.乙车从 地直达 地,两车同时到达 地.甲、乙两车距各自出发地的路程 (千米)与甲车出发后所用的时间 (时)的函数图象如图所示. (1)、求 的值;(2)、求甲车距它出发地的路程 与 之间的函数关系式;(3)、求两车相距120千米时乙车行驶的时间.26. 如图1所示,直线 与 轴负半轴, 轴正半轴分别交于 、 两点.
(1)、求 的值;(2)、求甲车距它出发地的路程 与 之间的函数关系式;(3)、求两车相距120千米时乙车行驶的时间.26. 如图1所示,直线 与 轴负半轴, 轴正半轴分别交于 、 两点. (1)、当 时,求直线 的解析式;(2)、在(1)的条件下,如图2所示,设 线段 延长线上一点,作直线 ,过 、 两点分别作 于点 , 于点 ,若 ,BN=3,求 的长;(3)、如图3,当 取不同的值时,点 在 轴正半轴上运动,分别以 、 为边,点 为直角顶点在第一、二象限内作等腰直角 和等腰直角 ,连接 交 轴于 点,当点 在 轴正半轴上运动时,试猜想 的面积是否改变;若不改变,请求出其值;若改变,请说明理由.(4)、如图3,当 取不同的值时,点 在 轴正半轴上运动,以 为边,点 为直角顶点,在第二象限作等腰直角 ,则动点 在直线上运动.(直接写出直线的解析式)
(1)、当 时,求直线 的解析式;(2)、在(1)的条件下,如图2所示,设 线段 延长线上一点,作直线 ,过 、 两点分别作 于点 , 于点 ,若 ,BN=3,求 的长;(3)、如图3,当 取不同的值时,点 在 轴正半轴上运动,分别以 、 为边,点 为直角顶点在第一、二象限内作等腰直角 和等腰直角 ,连接 交 轴于 点,当点 在 轴正半轴上运动时,试猜想 的面积是否改变;若不改变,请求出其值;若改变,请说明理由.(4)、如图3,当 取不同的值时,点 在 轴正半轴上运动,以 为边,点 为直角顶点,在第二象限作等腰直角 ,则动点 在直线上运动.(直接写出直线的解析式)