湖北省武汉市洪山区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 汉字是世界上最美的文字，形美如画、有的汉字是轴对称图形，下面四个汉字中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x - 2}{x + 1}$ 无意义，则x的取值等于（）

A、0 B、﹣1 C、﹣2 D、2

查看试题解析
3. 下列各式中计算结果为 $x^{6}$ 的是（）

A、 $x^{2} + x^{4}$ B、 $x^{8} - x^{2}$ C、 $x^{2} \cdot x^{4}$ D、 $x^{12} \div x^{2}$

查看试题解析
4. 在△ABC中，∠A＝x°，∠B＝(2x＋10)°，∠C的外角大小(x＋40)°，则x的值等于（）

A、15 B、20 C、30 D、40

查看试题解析
5. 下列等式中，从左到右的变形是因式分解的是（）

A、9－a²＝(3＋a)(3－a) B、x²－2x＝x(x－1)-x C、x＋2＝x(1＋ $\frac{2}{x}$ ) D、y(y－2)＝y²－2y

查看试题解析
6. 如图为正方形网格，则∠1+∠2+∠3=（）

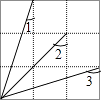A、105° B、120° C、115° D、135°

查看试题解析
7. 如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列3种割拼方法，其中能够验证平方差公式的是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析
8. 如图，在△ABC中，AB＝6，BC＝5，AC＝4，AD平分∠BAC交BC于点D，在AB上截取AE＝AC，则△BDE的周长为（）

A、8 B、7 C、6 D、5

查看试题解析
9. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．“其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每件椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
10. 如图，点A在y轴上，G、B两点在x轴上，且G（﹣3，0），B（﹣2，0），HC与GB关于y轴对称，∠GAH＝60°，P、Q分别是AG、AH上的动点，则BP＋PQ＋CQ的最小值是（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

11. △ABC的外角和等于．

查看试题解析
12. 纳秒 $(n s)$ 是非常小的时间单位， $1 n s = 10^{- 9} s$ ，北斗全球导航系统的授时精度优于 $20 n s$ ，用科学记数法表示 $20 n s$ 是．

查看试题解析
13. 若x²－mx＋9是一个完全平方式，则m的值是．

查看试题解析
14. 如图，在x、y轴上分别截取OA、OB，使OA＝OB，再分别以点A、B为圆心，以大于 $\frac{1}{2}$ AB的长度为半径画弧，两弧交于点C．若C的坐标为(3a，a＋10)，则a＝．

查看试题解析
15. 由奇数1，3，5，…，2021组成的和式： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{2019 \times 2021}$ ，化简后的结果为．

查看试题解析
16. 已知x²－3x－1＝0，则2x³－3x²－11x＋1＝．

查看试题解析

三、解答题

17. 利用乘法公式计算：

(1)、198×202

(2)、(2y＋1)(﹣2y－1)

查看试题解析
18. 因式分解：

(1)、2ax²－4axy＋2ay²

(2)、x²－2x－8

查看试题解析
19. 先化简，再求值： $(1 - \frac{x + 1}{x^{2} - 2 x + 1}) \div \frac{x - 3}{x - 1}$ ，其中x＝ $\frac{1}{2}$ ．

查看试题解析
20. 如图，已知△ABC的三个顶点的坐标分别为A(﹣2，3)，B(﹣3，2)，C(﹣1，1)

(1)、将△ABC向右平移7个单位，试作出平移后的△A₁B₁C₁ ，并写出点A₁的坐标；

(2)、在图中作出△ABC关于y轴对称的△A₂B₂C₂ ，观察可知△A₁B₁C₁与△A₂B₂C₂关于直线l对称，请写出直线l与x轴的交点D的坐标；

(3)、在x轴上找一点P，使PB＋PC最短，则Р点坐标为．

查看试题解析
21. 第一步：阅读材料，掌握知识．
要把多项式am＋an＋bm＋bn分解因式，可以先把它的前两项分成一组，并提出公因式a，再把它的后两项分成一组，提出公因式b，从而得： am＋an＋bm＋bn＝a(m＋n)＋b(m＋n)．这时，由于a(m＋n)＋b(m＋n)中又有公因式(m＋n)，于是可提出(m＋n)，从而得到(m＋n)(a＋b)，因此有： am＋an＋bn＋bn＝(am＋an)＋(bm＋bn)＝a(m＋n)＋b(m＋n)＝(m＋n)(a＋b)．这种方法称为分组法．

第二步：理解知识，尝试填空．

(1)、ab－ac＋bc－b²＝(ab－ac)＋(bc－b²)＝a(b－c)－b(b－c)＝．
第三步：应用知识，解决问题．

(2)、因式分解：x²y－4y－2x²＋8．
第四步：提炼思想，拓展应用．

(3)、已知三角形的三边长分别是a、b、c，且满足a²＋2b²＋c²＝2b(a＋c)，试判断这个三角形的形状，并说明理由．

查看试题解析
22. 新冠肺炎疫情暴发后，某医疗设备公司紧急复工，但受疫情影响，医用防护服生产车间仍有7人不能到厂工作，为了应对疫情，在每个工人每小时完成的工作量不变的前提下，已复工的工人加班生产，每天的工作时间由原来8个小时增加到10个小时．该公司原来每天能生产防护服800套，现在每天能生产防护服650套．

(1)、求该公司原来生产防护服的工人有多少人?

(2)、复工10天后，未到的7名工人到岗且同时加入了生产，每天生产时间仍然为10小时．为了支援灾区，公司复工后决定生产15500套防护服，问至少还需要多少天才能完成任务?

查看试题解析
23. 如图，△ABC为等边三角形，直线l经过点C，在l上位于C点右侧的点D满足∠BDC＝60°．

(1)、如图1，在l上位于C点左侧取一点E，使∠AEC＝60°，求证：△AEC≌△CDB；

(2)、如图2，点F、G在直线l上，连AF，在l上方作∠AFH ＝120°，且AF＝HF，∠HGF ＝120°，求证：HG＋BD＝CF；

(3)、在（2）的条件下，当A、B位于直线l两侧，其余条件不变时（如图3），线段HG、CF、BD的数量关系为．

查看试题解析
24.

(1)、如图1，平面直角坐标系中A(0，a)，B(a，0)(a>0)．C为线段AB的中点，CD⊥x轴于D，若△AOB的面积为2，则△CDB的面积为．

(2)、如图2，△AOB为等腰直角三角形，O为直角顶点，点E为线段OB上一点，且OB＝3OE，C与E关于原点对称，线段AB交x轴于点D，连CD，若CD⊥AE，试求 $\frac{A D}{D B}$ 的值．

(3)、如图3，点C、E在x轴上，B在y轴上，OB＝OC，△BDE是以B为直角顶点的等腰直角三角形，直线CB、ED交于点A，CD交y轴于点F，试探究： $\frac{C O - E O}{B F}$ 是否为定值?如果是定值，请求出该定值；如果不是，请求出其取值范围．

查看试题解析