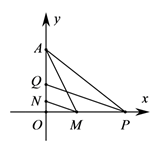湖北省鄂州市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 分式 有意义时 的取值范围是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 纳米(nm)是非常小的长度单位, .专家们研究证实,新型冠状病毒的直径大约为128纳米,即0.000000128米.该直径用科学记数法表示为( )米A、 B、 C、 D、5. 如图的三角形纸片中, , .沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,若 的周长为7cm,则 的长为( )
2. 分式 有意义时 的取值范围是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 纳米(nm)是非常小的长度单位, .专家们研究证实,新型冠状病毒的直径大约为128纳米,即0.000000128米.该直径用科学记数法表示为( )米A、 B、 C、 D、5. 如图的三角形纸片中, , .沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,若 的周长为7cm,则 的长为( )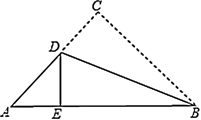 A、3cm B、4cm C、5cm D、6cm6. 一个等腰三角形的两边长分别为3、7,则它的周长为( )A、17 B、13或17 C、13 D、107. 我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲要早三百多年,我们把这个三角形称为“杨辉三角”.根据图中的数字排列规律 、 、 的值分别为( )
A、3cm B、4cm C、5cm D、6cm6. 一个等腰三角形的两边长分别为3、7,则它的周长为( )A、17 B、13或17 C、13 D、107. 我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲要早三百多年,我们把这个三角形称为“杨辉三角”.根据图中的数字排列规律 、 、 的值分别为( )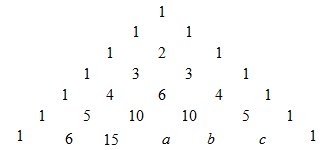 A、1,6,15 B、6,15,20 C、20,15,6 D、15,6,18. 用图1的面积可以验证多项式的乘法运算 ,那么用图2的面积可以验证的乘法运算是( )
A、1,6,15 B、6,15,20 C、20,15,6 D、15,6,18. 用图1的面积可以验证多项式的乘法运算 ,那么用图2的面积可以验证的乘法运算是( )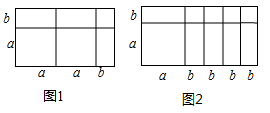 A、 B、 C、 D、9. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =10. 如图,在等腰 , ,点 为 内一点,且 ,若 长为6,则 的面积为( )
A、 B、 C、 D、9. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =10. 如图,在等腰 , ,点 为 内一点,且 ,若 长为6,则 的面积为( )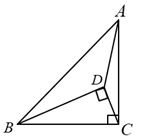 A、12 B、16 C、18 D、24
A、12 B、16 C、18 D、24二、填空题
-
11. 点 关于 轴对称的点的坐标是 .12. 若分式 的值为0,则 的值为.13. 一个 边形的内角和等于外角和的2倍,则其边数 为 .14. 如图, 的 和 的平分线 , 相交于点 ,若 ,则 的度数为 .
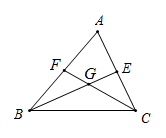 15. 计算 结果为 .16. 代数式 是个完全平方式,则m的值为17. 若关于 的分式方程 的解为正数,则常数 的取值范围是 .18. 如图,点 为线段 外一动点, , ,分别以 、 为边作等边 、等边 ,连接 .则线段 长的最大值为 .
15. 计算 结果为 .16. 代数式 是个完全平方式,则m的值为17. 若关于 的分式方程 的解为正数,则常数 的取值范围是 .18. 如图,点 为线段 外一动点, , ,分别以 、 为边作等边 、等边 ,连接 .则线段 长的最大值为 .
三、解答题
-
19. 分解因式:(1)、(2)、20. 先化简,再求值:
,其中 .
21. 将 的直角顶点 置于直线 上, ,分别过点 、 作直线 的垂线,垂足分别为点 、 ,连接 .若 , .求 的面积.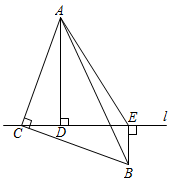 22. 在平面直角坐标系中的位置如图,点 ,点 ,点 .
22. 在平面直角坐标系中的位置如图,点 ,点 ,点 .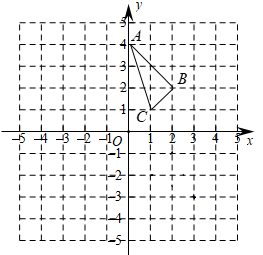
( 1 )将 向左平移4个单位得到 (点 、 、 的对应点分别为 、 、 ),画出 .
( 2 ) 和 关于 轴对称(点 、 、 的对称点分别为 、 、 ),画出 .
( 3 )在 轴上画出一点 ,使 的值最小,直接写出点 的坐标为_▲_.
23. 观察下列等式:, , .
将以上三个等式左、右两边分别相加得:
(1)、若 为正整数,猜想并填空: .(2)、计算 的结果为 .(3)、解分式方程: .24. 在 中, ,点 是直线 上一点(不与 、 重合),以 为一边在 的右侧作 ,使 , ,连接 .(1)、如图,当点 在线段 上,如果 ,则 度.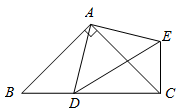 (2)、设 , .
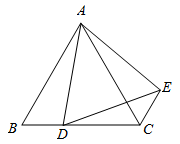
(2)、设 , .①如图,当点 在线段 上移动时, 、 之间有怎样的数量关系?请直接写出你的结论.
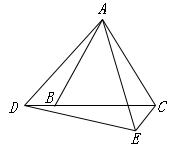
②如图,当点 在线段 的反向延长线上移动时, 、 之间有怎样的数量关系?请说明理由.
 25. 鄂州市2020年被评为“全国文明城市”.创文期间,甲、乙两个工程队共同参与某段道路改造工程.如果甲工程队单独施工,恰好如期完成;如果甲、乙两工程队先共同施工10天,剩下的任务由乙工程队单独施工,也恰好能如期完成;如果乙工程队单独施工,就要超过15天才能完成.(1)、求甲、乙两工程队单独完成此项工程各需多少天?(2)、若甲工程队单独施工 天,再由甲、乙两工程队合作天(用含有 的代数式表示)可完成此项工程.(3)、现在要求甲、乙两个工程队都必须参加这项工程.如果甲工程队每天的施工费用为2万元,乙工程队每天的施工费用为1.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,能使施工费用不超过61.5万元?26. 在平面直角坐标系中,点 ,点 ,点 ,且 、 满足 .(1)、点 坐标为 , 点 坐标为 , 是三角形.(2)、如图,过点 作射线 (射线 与边 有交点),过点 作 于点 ,过点 作 于点 ,过点 作 于点 交 轴于点 .
25. 鄂州市2020年被评为“全国文明城市”.创文期间,甲、乙两个工程队共同参与某段道路改造工程.如果甲工程队单独施工,恰好如期完成;如果甲、乙两工程队先共同施工10天,剩下的任务由乙工程队单独施工,也恰好能如期完成;如果乙工程队单独施工,就要超过15天才能完成.(1)、求甲、乙两工程队单独完成此项工程各需多少天?(2)、若甲工程队单独施工 天,再由甲、乙两工程队合作天(用含有 的代数式表示)可完成此项工程.(3)、现在要求甲、乙两个工程队都必须参加这项工程.如果甲工程队每天的施工费用为2万元,乙工程队每天的施工费用为1.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,能使施工费用不超过61.5万元?26. 在平面直角坐标系中,点 ,点 ,点 ,且 、 满足 .(1)、点 坐标为 , 点 坐标为 , 是三角形.(2)、如图,过点 作射线 (射线 与边 有交点),过点 作 于点 ,过点 作 于点 ,过点 作 于点 交 轴于点 .
①求证: ;
②求点 的坐标.
(3)、如图,点 是 轴正半轴上一动点, 的角平分线交 轴于点 ,点 为线段 上一点,过点 作 交 轴于点 ;若 ,请探究线段 、 、 三者之间的数量关系,并证明你的结论.