河南省安阳市滑县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 化简分式的结果为( )
A、 B、+ C、 D、2. 如图,线段 是 的高的是( )A、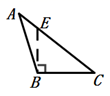 B、
B、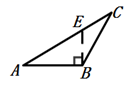 C、
C、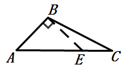 D、
D、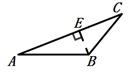 3. 计算 的结果是( )A、 B、 C、 D、4. 若 是一个完全平方式,则a的值为( )A、20 B、-20 C、±20 D、±105. 如图,在 中, , 平分 ,若 , ,则 的面积为( )
3. 计算 的结果是( )A、 B、 C、 D、4. 若 是一个完全平方式,则a的值为( )A、20 B、-20 C、±20 D、±105. 如图,在 中, , 平分 ,若 , ,则 的面积为( )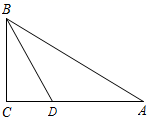 A、3 B、6 C、8 D、126. 下列尺规作图,能确定 是 的中线的是( )A、
A、3 B、6 C、8 D、126. 下列尺规作图,能确定 是 的中线的是( )A、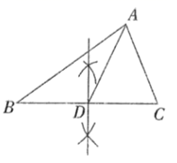 B、
B、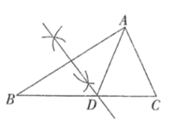 C、
C、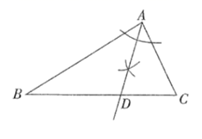 D、
D、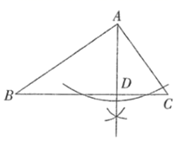 7. 如图,在 中, , 为 边上的一点,点 在 边上, ,若 ,则 的度数为( )
7. 如图,在 中, , 为 边上的一点,点 在 边上, ,若 ,则 的度数为( )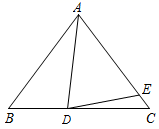 A、20° B、15° C、10° D、30°8. 如图,点 是 的 , 的平分线的交点, 交 于点 , 交 于点 ,若 的周长为 ,那么 的长为( )
A、20° B、15° C、10° D、30°8. 如图,点 是 的 , 的平分线的交点, 交 于点 , 交 于点 ,若 的周长为 ,那么 的长为( )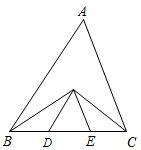 A、 B、 C、 D、9. 如图,在 中, , ,边 的垂直平分线交 于点 ,垂足为点 ,连接 ,若 ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, , ,边 的垂直平分线交 于点 ,垂足为点 ,连接 ,若 ,则 的长为( )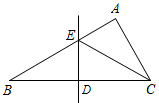 A、3 B、 C、4 D、10. 若 ,则 , , 的大小关系是( )A、 B、 C、 D、
A、3 B、 C、4 D、10. 若 ,则 , , 的大小关系是( )A、 B、 C、 D、二、填空题
-
11. 若 , ,则 ; .12. 一个n边形的每个内角都等于140°,则n=.13. 点 和点 关于 轴对称,则 .14. 甲乙两地相距5km,汽车从甲到乙,速度为 km/h,可按时到达,若每小时多行驶 km,则汽车提前h到达.15. 对于有理数 , ,定义 :当 时, ;当 时, .若 ,则 的值为 .
三、解答题
-
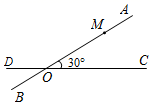
16. 先化简,再求值: ,其中 .17.(1)、分解因式:2ax2﹣8ay2 .(2)、解分式方程: .18. 如图,两条笔直的公路 , 相交于点 , 为30°,指挥中心 设在 路段上,与 地的距离为20千米.一次行动中,王警官带队从 地出发,沿 方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在9千米之内进行通话,通过计算判断王警官在行进过程中能否与指挥中心用对讲机通话.
 19. 如图,已知 , , 与 交于 , .连接 .
19. 如图,已知 , , 与 交于 , .连接 .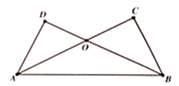
求证: 是等腰三角形.
20. 如图1,在 中, ,点 是 的中点,连接 ,点 在 上.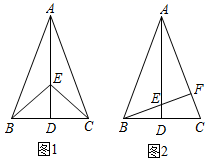 (1)、连接 , ,求证: ;(2)、如图2,若 的延长线交 于点 ,且 , ,原题设其他条件不变.求证: .21. 从边长为 的正方形中剪掉一个边长为 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)、连接 , ,求证: ;(2)、如图2,若 的延长线交 于点 ,且 , ,原题设其他条件不变.求证: .21. 从边长为 的正方形中剪掉一个边长为 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).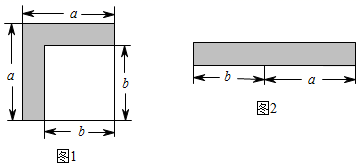 (1)、上述操作能验证的等式是;(2)、运用(1)中的结论,完成下列各题:
(1)、上述操作能验证的等式是;(2)、运用(1)中的结论,完成下列各题:①已知: , ,求 的值;
②计算: .
22. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?23. 已知: ,点 是 平分线上一点,点 在射线 上,作 ,交直线 于点 ,作 于点 .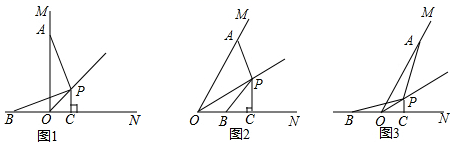 (1)、观察猜想:如图1,当 时, 和 的数量关系是 .(2)、探究证明:如图2,当 时,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请直接写出 , 之间另外的数量关系.(3)、拓展延伸:如图3,当 ,点 在射线 的反向延长线上时,请直接写出线段 , 及 之间的数量关系: .
(1)、观察猜想:如图1,当 时, 和 的数量关系是 .(2)、探究证明:如图2,当 时,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请直接写出 , 之间另外的数量关系.(3)、拓展延伸:如图3,当 ,点 在射线 的反向延长线上时,请直接写出线段 , 及 之间的数量关系: .