贵州省铜仁市沿河土家族自治县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-17 类型:期末考试
一、单选题
-
1. 下列式子中是分式的是( )A、 B、 C、 D、2. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、3. 中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项,已知显微镜下某种疟原虫平均长度为0.0000015米,该长度用科学记数法可表示为( )A、 米 B、 米 C、 米 D、 米4. 下列计算正确的是( )A、 B、 C、 D、5. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、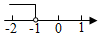 D、
D、 6. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
6. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
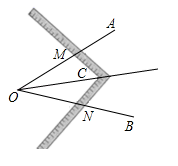 A、SSS B、SAS C、ASA D、AAS7. 已知实数 在数轴上的对应点位置如图所示,则化简 的结果是( )
A、SSS B、SAS C、ASA D、AAS7. 已知实数 在数轴上的对应点位置如图所示,则化简 的结果是( )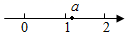 A、 B、 C、1 D、8. 在 , ,0, ,0.010010001, ,-0.333…, , 3.14,1.2121121112…(相连两个2之间1的个数逐次加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个9. 一艘轮船顺水航行40km所用的时间与逆水航行30km所用的时间相同,若水流速度为3 km/h,求轮船在静水中的速度.设轮船在静水中的速度为xkm /h,根据题意列方程得( )A、 B、 C、 D、10. 如图,已知 ,点 , , ,…,在射线 上,点 , , , ,…,在射线 上, , , ,…,均为等边三角形.若 ,则 的边长为( )
A、 B、 C、1 D、8. 在 , ,0, ,0.010010001, ,-0.333…, , 3.14,1.2121121112…(相连两个2之间1的个数逐次加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个9. 一艘轮船顺水航行40km所用的时间与逆水航行30km所用的时间相同,若水流速度为3 km/h,求轮船在静水中的速度.设轮船在静水中的速度为xkm /h,根据题意列方程得( )A、 B、 C、 D、10. 如图,已知 ,点 , , ,…,在射线 上,点 , , , ,…,在射线 上, , , ,…,均为等边三角形.若 ,则 的边长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
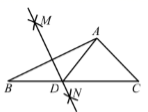
11. -8的立方根是; 的平方根是 .12. 若(m+1)0=1,则实数m应满足的条件 .13. 方程 的解是14. 等腰三角形一腰上的高与另一腰的夹角是36°,则这个等腰三角形顶角的度数是 .15. 已知 =3,则代数式 的值是 .16. 不等式组 的最小整数解是.17. 如图,在 中, ,分别以点 为圆心,大于 的长为半径画弧,两弧相交于点 作直线 ,交 边于点 ,连接 ,则 的周长为.
 18. 根据 , , , …的规律,则可以得出 … 的末位数字是 .
18. 根据 , , , …的规律,则可以得出 … 的末位数字是 .三、解答题
-
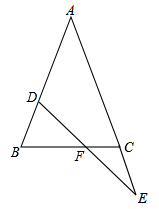
19.(1)、计算(2)、先化简,再求值: , 从0,1,2,3四个数中适当选取.20. 已知 .(1)、求 , 的值;(2)、求 的算术平方根.21. 一幢学生宿舍楼有一些空宿舍,现有一批学生要入住,若每间住5人,则有25人无法入住;若每间住10人,则有1间房不空也不满.求空宿舍的间数和这批学生的人数.22. 已知在 中, , 在 上, 在 的延长线上, 交 于 ,且 ,求证: .
 23. 模拟应用在进行二次根式的除法运算时,我们有时会碰上如 , , 这样的式子,其实我们还可以将其进一步化简:
23. 模拟应用在进行二次根式的除法运算时,我们有时会碰上如 , , 这样的式子,其实我们还可以将其进一步化简:(一);
(二);
(三).
以上这种化简的步骤叫分母有理化.
还可以用以下方法化简:
(四).
(1)、请用不同的方法化简: .①参照(三)式得 ;
②参照(四)式得 .
(2)、化简 .24. 为抗击新冠状肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A、B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A、B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.(1)、求A、B两车间每天分别能生产口罩多少万个?(2)、如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求生产这批口罩该公司共创造利润多少万元?25. 如图,在 中, , ,点 在线段 上运动(点 不与点 , 重合),连接 ,作 , 交线段 于点 .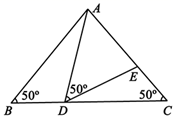 (1)、当 时, °, °, °;(2)、当 等于多少时? ≌ ,请说明理由.(3)、在点 的运动过程中,请直接写出当 是等腰三角形时 的度数.
(1)、当 时, °, °, °;(2)、当 等于多少时? ≌ ,请说明理由.(3)、在点 的运动过程中,请直接写出当 是等腰三角形时 的度数.